Be sure to check back often, because assignments may change!
(Last modified: Sunday, December 5, 2010, 9:17 AM )

All section and page numbers refer to sections from Calculus: Early Transcendental Functions, 3rd Edition, by Smith and Minton.

I'll use Maple syntax for some of the mathematical notation on this page. (Paying attention to how I type various expressions is a good way to absorb Maple notation). I will not use it when I think it will make the questions too difficult to read.

Due Monday 11/1 at 8am

Section 3.7: Optimization

To read: Thru Example 3.7.3. Really read through these examples carefully, paying attention to why the authors are doing each step. In Example 3.7.3, pay particular attention to the transitoin from the distance function d(x) to the function to be optimized, f(x)=[d(x)]² -- this is a useful technique

Reading questions:

In Example 3.7.1 and 3.7.2, the authors caution us not to simplify the function to be maximized out of habit ; although they omit this caution in Example 3.7.3 they again refrain from expanding the function to be maximized.
1. In Example 3.7.1, would expanding A(x) have made any of the steps that followed simpler? Would it have made any of the steps harder?
2. In Example 3.7.2, would expanding V(x) have made any of the steps easier? Harder?

Reminder:

• Monday is the deadline for receiving full credit on the Differentiation Exam.
• As usual, put plenty of time and effort into studying for Exam 2; spreading your studying time out over several days is harder for some to plan, but much more effective than packing it into one or two days.

Due Wednesday 11/3 at 8am

Bring Questions for Exam 2

No Reading Questions Today

Reminder:

• As usual, take advantage of all the Kollett Center has to offer, as well as my office hours.
• Get questions on PS 9 out of the way before class as much as possible, so you can be focusing on reviewing everything for the exam.
• Once again, you may have a "cheat sheet", consisting of notes handwritten by you on one side of an 8 1/2 x 11 (or smaller) piece of paper.
• You may begin taking the exam at 12:30pm Thursday.
• If you have not yet passed the Differentiation Exam, the next deadline is Monday 11/8 at 4pm, for 90% -- study for Exam 2 now, then get back to working on the Differentiation Exam.

Due Friday 11/5 at 8am

Section 3.7: Optimization (continued)

To read: Finish the section. Pay close attention to Remark 3.7.1.

Reading questions:

1. In Example 3.7.5,
   1. what physically does the quantity 2πr² represent? How about 2πrh?
   2. The derivative A'(r) is not defined at r=0. Why is 0 not a critical number for A(r)?
   3. the result the authors arrived at for the values that minimize the amount of material used in a can do not reflect the reality of the design of most 12 oz cans. Did you notice any unrealistic assumptions that were made while working through the problem that may explain this difference?
2. In Example 3.7.6, why are the only critical numbers those values of x where C '(x)=0?
3. For each of the following, answer True or False, and give a brief explanation or example for your choice
   1. If there is only one critical point, it must be the minimizer or maximizer that you are seeking.
   2. If there is only one critical point, it must be a local extremum.
   3. If there is only one local extremum, it must be an absolute extremum as well.

Reminder:

• Begin working on WW 10 and PS 10 (another group problem set). Once again, switch partners, be primary author if you weren't last time, and don't split up the problems.
• For those who are still working on the Differentiation Exam, the deadline for receiving 90% is Monday 11/8 at 4pm.

Due Monday 11/8 at 8am

Handout on Taylor Polynomials (available on OnCourse page)

To read: All. I know adjusting to the different style and language can take effort, but be patient

Reading questions:

1. Why might finding the Taylor polynomial of a function be useful?
2. In your own words, briefly explain the idea (not just the steps) of building a Taylor polynomial for a function f(x).

Submit answers through OnCourse

Reminder:

• The deadline for receiving 90% on the Differentiation Exam is Monday at 4:00pm.

Due Wednesday 11/10 at 8am

Handout on Taylor Polynomials (continued) (available on OnCourse page)
Section 4.2: Sums and Sigma Notation

(Note that we are skipping Sections 3.8, 3.9, and 4.1)

To read: Re-read the section on Taylor polynomials carefully. Back in your own textbook, you may skip the first 1.5 pages of Section 4.2 -- we're not dealing with the ideas of chapter 4 yet, but I thought that the notation introduced in this section could help with Taylor polynomials. Begin reading in the middle of page 355, with the sentence that reads "We begin by introducing some notation. " Read through Example 2.3, and also just read the statement of Theorem 2.2.

Reading questions:

1. Write 2^-1+3^-1+4^-1+5^-1+6^-1+7^-1+8^-1+9^-1+10^-1+11^-1+12^-1 in summation notation.
2. Write out the terms (do not evaluate) from expanding
   
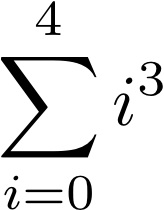
3. What do you think the purpose of summation (sigma) notation is?
4. So that I know how much detail to go into ... have you seen sigma (summation) notation before? How well do you feel like you understand it?

Reminder:

• Bring questions on PS 10.
• Remember to put a star next to the primary author's name.
• If you are still working on the Differnetiation Exam, the next deadline is 11/29, to receive 75%.

Due Friday 11/12 at 8am

Introduction to Chapter 4
Section 4.3: Area

To read: Skim through all. Don't get too hung up on the notation and the vocabulary -- at this point, I'm mainly concerned with the big ideas of undertanding using rectangles to approximate area.

Reading questions:

1. Briefly describe how to approximate the area between a curve and the x-axis over an interval [a,b].
2. In Equation 4.3.1,
   what do f(x_i), Δx, and n represent?
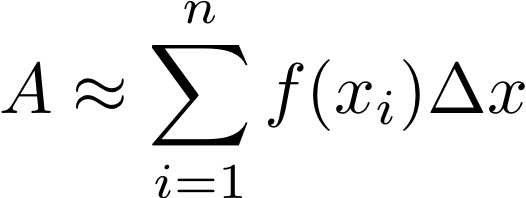
3. Suppose f is a positive decreasing function. Does a right sum (that is, a Riemann Sum using the right endpoints) over- or under-estimate the area between f(x) and the x-axis? How about a left sum?

• Begin WW 11 and PS 11.

Due Monday 11/15 at 8am

Section 4.4: The Definite Integral

To read: All

Reading questions:

1. In Example 4.2, interpret the definite integral (that is, the limit of the Riemann sum) as area.

Submit answers through OnCourse

Due Wednesday 11/17 at 8am

Section 4.4: The Definite Integral

To read: All

Reading questions:

1. Explain why Theorem 4.4.1, which states that if f is continuous over the closed interval [a,b], then f is integrable on [a,b], seems plausible to you.
2. Explain why Part ii of Theorem 4.4.2 makes sense graphically.

Reminder:

• Bring remaining questions on PS 11 to class.
• Exam 3 will be on Thursday 12/2, the Thursday after Thanksgiving Break.

Due Friday 11/19 at 8am

Section 4.4: The Definite Integral (continued)

To read: None

No Reading Questions Today!

Submit answers through OnCourse

Reminder:

• Begin working on WW 12. As usual, because of the exam this assignment will not be graded, but the material on it will be covered on the exam.
• If you are still working on the Differentiation Exam, the deadline to receive 75% on it is the Monday after Thanksgiving Break, Monday 11/29 at 4pm.

Due Monday 11/22 at 8am

Section 4.5: The Fundamental Theorem of Calculus

To read: None yet - because I plan on approaching the section in a slightly different order than the text does, I think you'll get the most out of the reading if you wait and read the whole section for next Monday.

No Reading Questions: Today

Reminder:

• If you are still working on the Differentiation Exam, the deadline to receive 75% on it is the Monday after Thanksgiving Break, Monday 11/29 at 4pm.

Due Wednesday 11/24 at 8am

Thanksgiving Break

No Reading Questions Today, Of Course

Due Friday 11/26 at 8am

Thanksgiving Break

No Reading Questions Today

Due Monday 11/29 at 8am

Section 4.5: The Fundamental Theorem of Calculus

To read: All.

Reading questions:

1. Does every continuous function f have an antiderivative? If so, what is it? If not, why not?
2. If you're given instantaneous velocity, how do you find net distance traveled over an interval of time?

Submit answers through OnCourse

Reminders:

• The deadline to receive 75% on the differentiation exam is Monday at 4pm.

Due Wednesday 12/1 at 8am

Bring Questions for Exam 3

No Reading Questions Today

Reminders:

• Visit my office hours and visit the Kollett Center while clearing up questions before the exam!
• Get questions on WW 12 out of the way before class. WW12 should be done before class so that you can focus on reviewing.
• As usual, you may have a "cheat sheet", consisting of handwritten notes on one side of an 8 1/2 x 11 (or smaller) piece of paper for the exam.
• As before, you may begin taking the exam at 12:30pm Tuesday.

Due Friday 12/3 at 8am

Section 4.1: Antiderivatives

To read: All. Pay particular attention to the concept of the indefinite integral; the rest of the section should be review so you can probably just skim the rest.

Reading questions:

1. If F and G are both antiderivatives of f(x), how are F(x) and G(x) related to each other algebraically? How are they related to each other graphically?
2. What is the difference between an antiderivative and an indefinite integral?

Submit answers through OnCourse

Reminders:

• Begin WW 13.
• If you are still working on the Differentiation Exam, the last day to receive any credit (50%) is the last day of classes (Friday 12/10), at 3pm.

Due Monday 12/6 at 8am

Section 4.6: Integration by Substitution

To read: All except for Example 4.6.8

Reading questions:

1. What do e^x2 from Example 4.6.1, (x³+5)¹⁰⁰ from Example 4.6.2, cos(x²) from Example 4.6.3, (3sin x +4)⁵ from Example 4.6.4, and sin(√x) from Example 4.6.5 all have in common?
2. Looking again at these same functions and examples -- what did the choice of u have in common in each?
3. When calculating antiderivatives or indefinite integrals, how can you always check whether you result is correct (without using a computer or a calculator?)

Submit answers through OnCourse

Due Wednesday 12/8 at 8am

Section 4.6: Substitution

To read: Review

No Reading Questions Today

Reminders:

• I will answer questions on WW 13 on Thursday (or possibly Friday) rather than on Wednesday as is usual.

Due Friday 12/10 at 8am

The Big Picture

No Reading Questions Today
Reminders:

• The deadline to receive 50% on the Diff Exam is Friday at 3pm.
• If I did not deal with questions on WW 13 on Thursday, then bring them to class Friday.

Janice Sklensky
Wheaton College
Department of Mathematics and Computer Science
Science Center, Room 101A
Norton, Massachusetts 02766-0930
TEL (508) 286-3973
FAX (508) 285-8278
jsklensk@wheatonma.edu