Drawing a square in perspective
| Point | x | y | z | d | x' | y' | New Point |
| A | 10 | 15 | 30 | 20 | 4 | 6 | A' |
| B | 15 | 15 | 30 | 20 | 6 | 6 | B' |
| C | 15 | 15 | 35 | 20 | 5.45 | 5.45 | C' |
| D | 10 | 15 | 35 | 20 | 3.64 | 5.45 | D' |
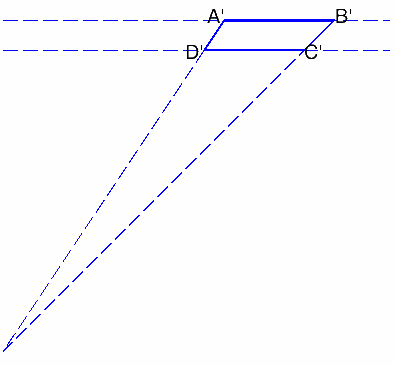
When we plot the perspective images of the four corners of the square, we see the following:
Notice that it does look like a 3d square, lying parallel to but above the floor! The front is the thicker blue.
Observing behavior, starting to hypothesize
The original 3 dimensional square has 2 pairs of parallel edges, of course. How can you tell which are the parallel pairs just by looking at the coordinates?
| Point | x | y | z |
| A | 10 | 15 | 30 |
| B | 15 | 15 | 30 |
| C | 15 | 15 | 35 |
| D | 10 | 15 | 35 |
- The edge from A to B occurs 15 units above the "floor", 30 units back from the picture plane, and x goes from 10 to 15.
- The edge from B to C is again 15 units above the floor, and is 15 units over to the right. It goes from being 30 units back to being 35 units back.
- The edge from C to D is also 15 units above the floor. It is 35 units back, and goes from 10 to 15 units to the right. Thus it is always 5 units further back than the edge from A to B.
- The edge from D to A is again 15 units up, and is always 10 units to the right, but goes from being 30 units back to being 35 units back.
All four edges are a constant distance above the floor (15 units), so they're parallel to the floor. But that doesn't mean they're parallel to each other!
AB and CD are a constant distance back from the picture plane (30 and 35 units back, respectively), so they're parallel to the picture plane as well as being parallel to the floor. Because they are parallel to both, they are parallel to each other.
BC and DA are a constant distance from the "side wall" (the yz plane), so they're parallel to that plane as well as being parallel to the floor. Because they are parallel to both, they are parallel to each other. They are also orthogonal (i.e. perpendicular) to the picture plane
How do these parallel lines appear in our 2 dimensional representation?
The two edges which were parallel to the picture plane (as well as to each other) remain parallel to each other in the perspective image.
The two edges which were orthogonal to the picture plane (but were parallel to each other) do not remain parallel in the image. If we extend them out, they eventually intersect.
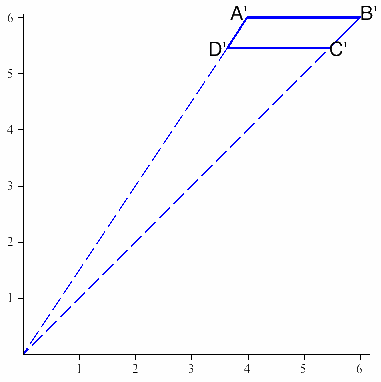
Where do the lines orthogonal to the picture plane intersect?
When we look at the image along with the coordinate axes, we see that when we extend these two lines, they not only intersect, but they intersect at the origin:
Is this a coincidence? Is it specific to this example? Do all lines that aren't parallel to the picture plane intersect at the origin? If not, do all lines that are orthogonal to the picture plane intersect at the origin?
Next!
Back to Perspective | Back to In Class Work