

The Great Pyramid of Giza
When we look at a pyramid, there are a lot of dimensions we could measure and take the ratio of:
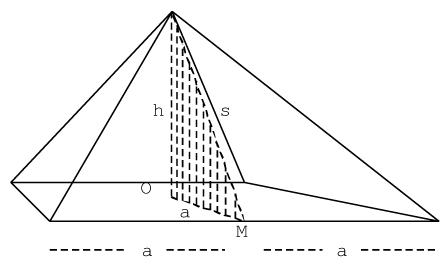
Measured Dimensions of the Great Pyramid:
- h= height of pyramid = 481.4'
- average length of side of base = 755.76'
- a = distance from center to midpoint of side ≈ 755.76/2 ≈ 377.88
- s = slant height = distance from top to midpoint of side =?
Looking for ratios in the Great Pyramid:
- Use the Pythagorean Theorem to find the slant height s of the pyramid.
Remember: (leg 1)2 + (leg 2)2=(hypotenuse)2. - Find the ratio of the slant height, s, to half the length of the base, a.
- Is the ratio s/a within our acceptance range for the Golden Ratio?
- How far off is s/a from the Golden Ratio? That is, what percentage of the Golden Ratio is s/a?
(Either use (1+sqrt(5))/2 for the Golden Ratio, or use 1.61803.) - Find the ratio of the height h to half the length of the base, a.
- Find the square root of the Golden Ratio. Again, at least use 1.61803, if not the exact value of the Golden Ratio, (1+sqrt(5))/2.
- How far off is h/a from the square root of the Golden Ratio? That is, what percent of the square root of the Golden Ratio is h/a?
Questions on how and why the Golden Ratio and Pi seem to appear in the design of the Great Pyramid
Back to the Golden Ratio | Back to In-Class