• Getting Started:
  1. Pick any point in or on your triangle. Place a dot at this point. This is the seed position.
  2. Roll the die.
  3. Put a second dot half the distance between your original circle and the vertex of the triangle that's labeled with the number you rolled on the die.

  4. Go to Step 2.
  Repeat this process 7 or 8 times before moving on to the next step.
  After 8 or 9 iterations, erase all but the last dot you made (the first iterations were to work out the kinks and get the pattern settled):

• Continuing play: Play just as above. In other words:
  1. Locate your current position.
  2. Roll the die.
  3. Use the halfway ruler (see below) to find the point that's halfway in between your current position and the vertex of the triangle that's labeled with the number you rolled on the die.

     For instance, if you roll a 6, put a new dot halfway between the last dot you made and the vertex labelled with a 6.

     Mark that point on the transparency.
     This is your new current position.

  4. Return to step 2.
  Do this for at least 10 iterations.

• Using the halfway ruler to measure half the distance: Notice that the middle of the ruler is marked with a *, and that at equal distances on either side of that halfway point are the markings A, B, C, with other lines in between, so that the two sides are reflections of each other.

  To find the point halfway in between your current position and the vertex corresponding to the number you rolled: Arrange the ruler so that the same ruler-marking is on (or nearest to) both your current position and the vertex you're heading toward. Put your next mark at the *.

• What do we end up with?
  

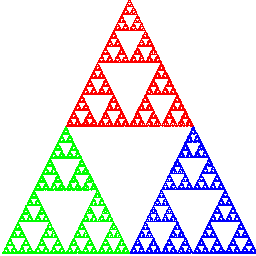
Why does the chaos game lead to the Sierpinski gasket?

Back to Fractals | Back to Inclass