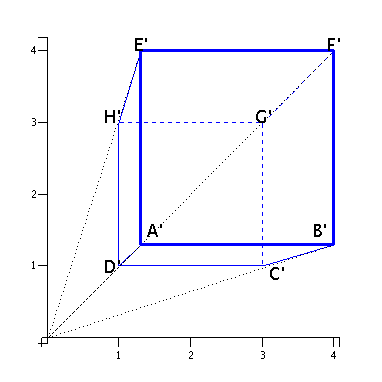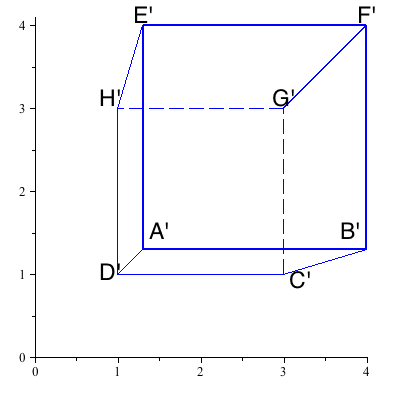
| Base=ABCD | Top=EFGH | ||||||
| Point | x | y | z | Point | x | y | z |
| A | 2 | 2 | 4 | E | 2 | 6 | 4 |
| B | 6 | 2 | 4 | F | 6 | 6 | 4 |
| C | 6 | 2 | 8 | G | 6 | 6 | 8 |
| D | 2 | 2 | 8 | H | 2 | 6 | 8 |
Using that the viewer's eye is 8 units back from the picture plane (so d=8), and using the perspective theorem, we find the perspective images of these points:
| Point | x | y | z | d | x' | y' | New Point |
| A | 2 | 2 | 4 | 8 | 1.3 | 1.3 | A' |
| B | 6 | 2 | 4 | 8 | 4 | 1.3 | B' |
| C | 6 | 2 | 8 | 8 | 3 | 1 | C' |
| D | 2 | 2 | 8 | 8 | 1 | 1 | D' |
| E | 2 | 6 | 4 | 8 | 1.3 | 4 | E' |
| F | 6 | 6 | 4 | 8 | 4 | 4 | F' |
| G | 6 | 6 | 8 | 8 | 3 | 3 | G' |
| H | 2 | 6 | 8 | 8 | 1 | 3 | H' |
When we graph these points on standard 2-dimensional (xy) axes, we see that the image looks like this:

Again, the 2 sets of four edges which were parallel to each other and to the picture plane remain parallel to each other in the perspective image, but the set of four edges which are parallel to each other but orthogonal to the picture plane are not parallel to each other in the image!
Furthermore, when we extend these lines, we see that not only are they not parallel, but all four intersect in the same point, and that point is (once again) the origin.