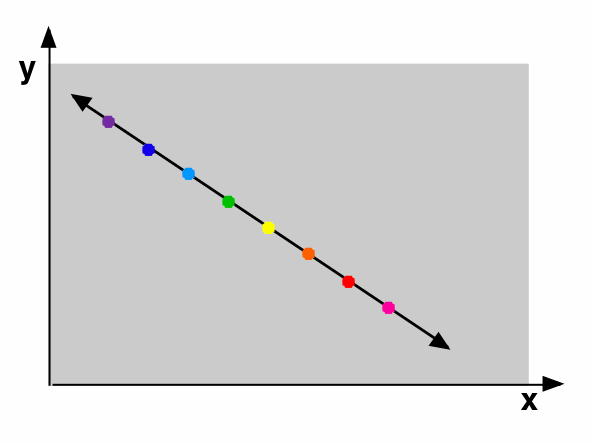
Further Pondering
Next, suppose a viewer is looking at a line parallel to the window/picture plane that he/she is facing straight on. Now what does the viewer see? Approaching it the same way, we see the following:
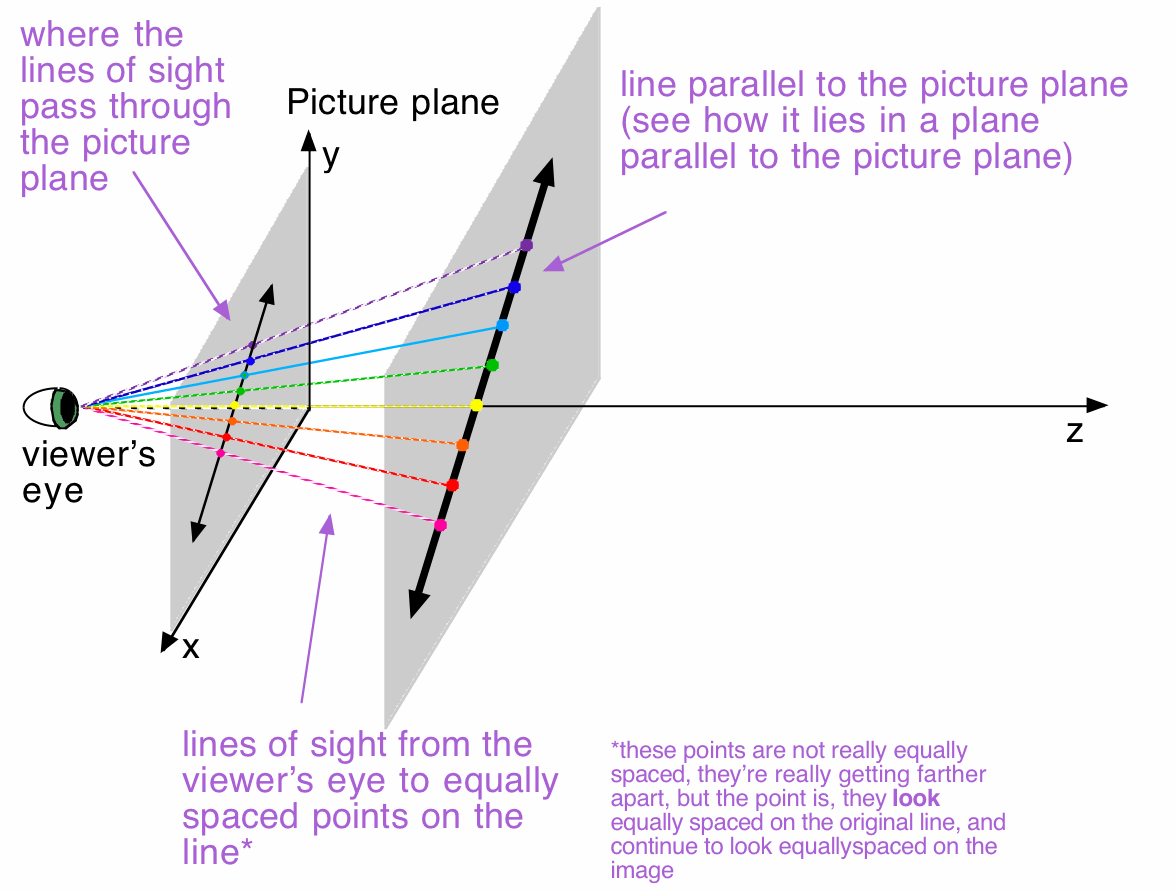
Partial Side View (so you can see all three axes)
Straight-on Side View (so we can't see the x-axis)
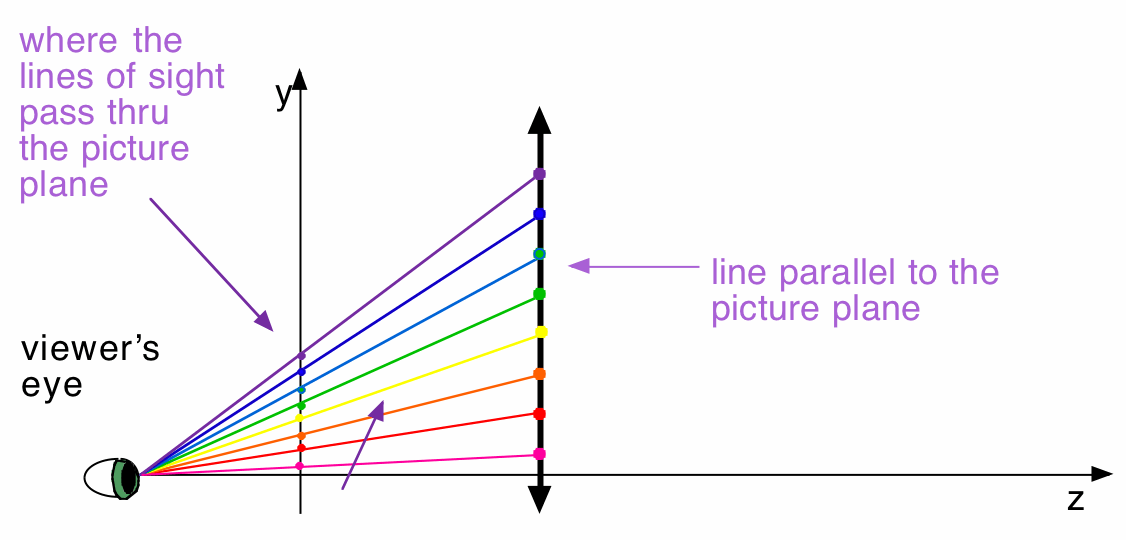
Here, we can clearly see that the y-coordinates of points that are equally spaced on the 3D line that the viewer is looking at remain equally spaced on the y-axis of the picture plane.
Straight-on Top View (so we can't see the y-axis)
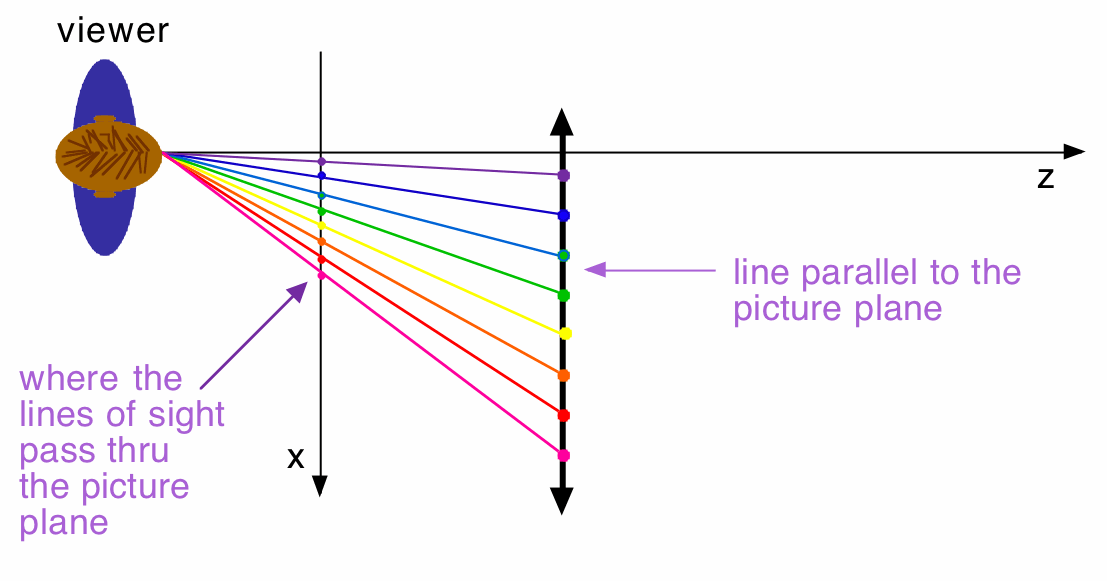
And here, we can see that the same holds true for the x-coordinates of the perspective images.
Front View - what the viewer sees
Let's again rotate around to see what the viewer sees:
Points on the line again remain in a line. Furthermore, points on this line which are the same distance apart in real-life remain the same distance apart in the perspective image (although of course that distance is smaller than in real-life). And finally, the perspective image of this line will go on and on forever - it does not vanish. For as long as the viewer is looking at the line, his/her line of sight will intersect with the plane of the picture. The instant that the line appears to vanish to the viewer is the instant at which the viewer's line of sight becomes parallel to the line ... which is parallel to the picture plane. And if the viewer's line of sight is parallel to the picture plane, there will be no image point anyway - he/she's not looking at the picture.
Conclusion:
| The perspective images of lines parallel to the picture plane appear exactly as they do in real-life, and have no vanishing point. |
Next!
Back to Perspective | Back to In Class Work