Partial Side View (showing all three axes)
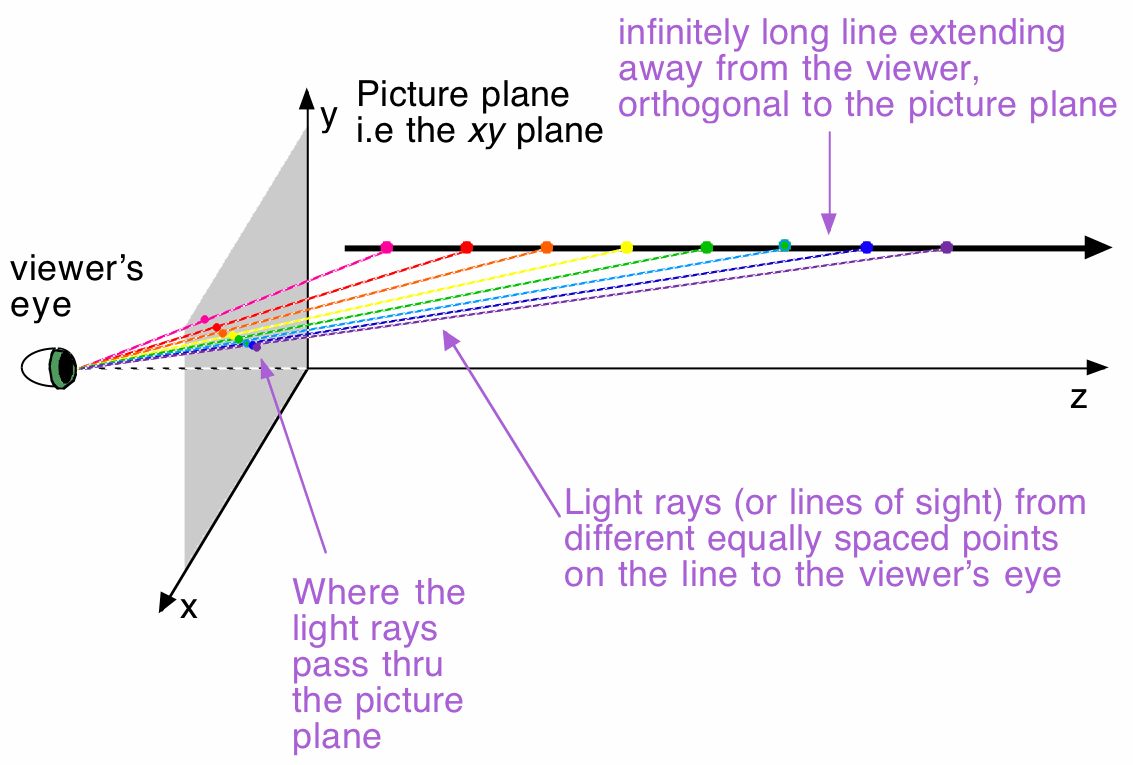
Suppose a viewer is looking at a line orthogonal to the window/picture plane that he/she is facing straight on. What does the viewer see? We can figure it out by placing the viewer's eye on the negative z-axis, and by drawing a line orthogonal to the xy-plane, which represents the picture plane/window. We then draw a line orthognal to the picture plane, place several different colored points on that line, and draw the viewer's line of sight to each of the points. We then mark where those lines of sight cross the picture plane. In essence, this creates a view from above and off to the side of what's going on.

It looks as if the points where the light rays cross the picture plane form a line, so that the 2D perspective image will be a line. It also looks as if the 2D images of points farther out on the 3D line will be closer to the origin than the images of closer points. Let's look at this from a few other views.
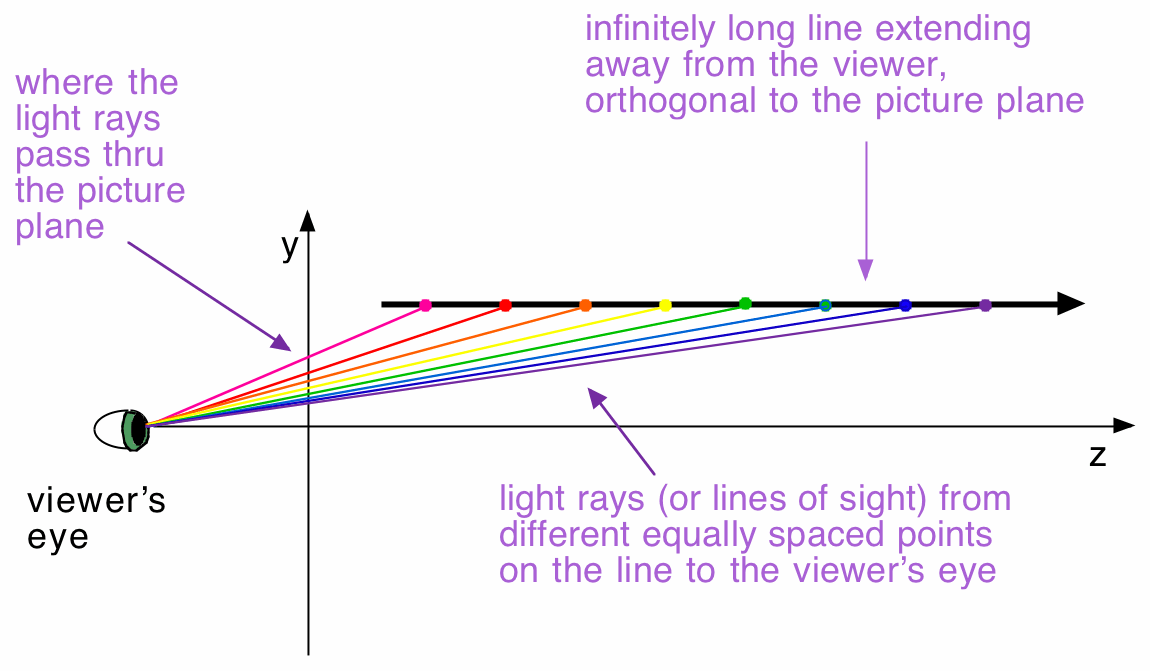
In this diagram, it is very clear that the farther out along the line the viewer looks, the lower the image point will be. Will these image points ever go below the z-axis? Remember - image points are where light rays, or lines of sight, connecting the viewer's eye to the line cross the picture plane. In this diagram, as long as the viewer is looking at the line at all, the line of sight will be angling up at least a little bit, and so the image point will be above the z-axis.
If you think of the viewer's gaze as moving farther and farther out along the line until he/she can't see the line anymore, the instant the viewer can't see the line anymore is the instant the viewer's line of sight is parallel to the line he/she had been looking at.
Since the line he/she had been looking at is orthogonal (perpendicular) to the y-axis, the instant at which the line vanishes is the instant at which the line of sight is orthogonal to the y-axis.
And since the viewer's eye is on the z-axis, when the viewer's line of sight is perpendicular to the y-axis, that line of sight will go right through y=0. Thus the real 3D line appears to vanish when y=0.
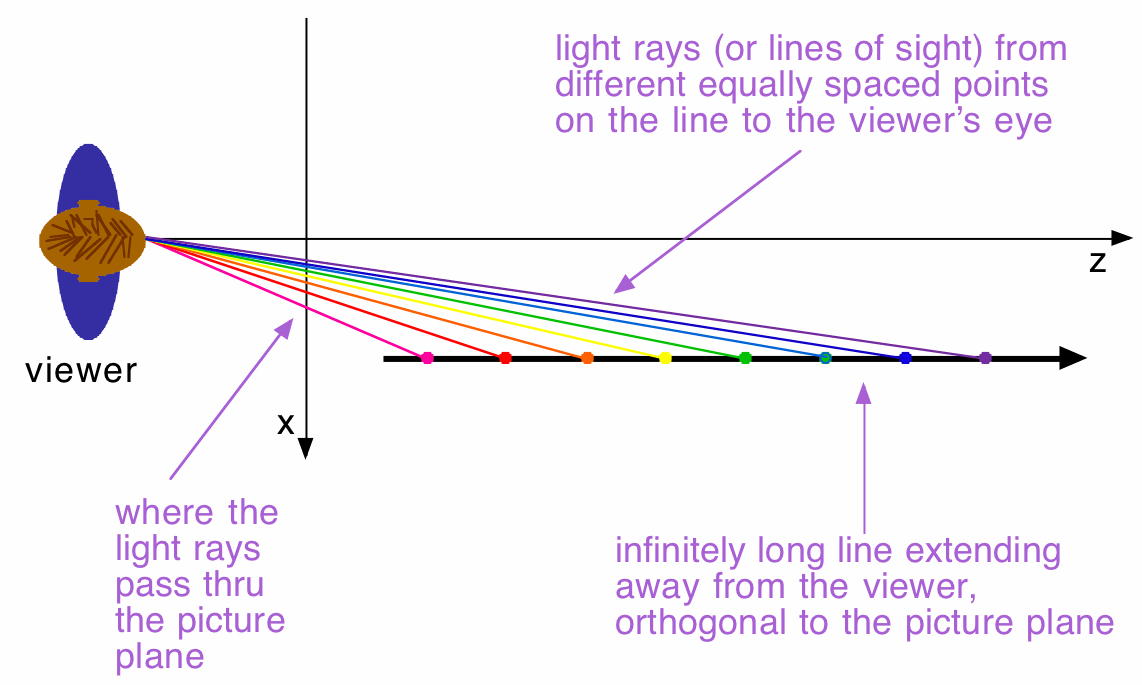
In this top-view, it is again clear that the farther out along the line the viewer looks, the closer the image point will be to the z-axis.
Again, as long as the viewer is looking at the line at all, the line of sight will be angling to the viewer's right at least a little bit, and so the image point will be to the right of the z-axis (to the viewer).
If you again think of the viewer's gaze as moving farther and farther out along the infinite line, the viewer can see the line as long as the line of sight intersects the line; the line vanishes at the instant the line of sight becomes parallel to the line.
And since the line is also orthogonal (perpendicular) to the x-axis, the instant at which the line vanishes is the instant at which the line of sight is orthogonal to the x-axis, so the line of sight will go right through x=0. Thus the real 3D line appears to vanish when x=0.
What does the viewer see? In other words, where could we draw on the picture plane to mimic the points on the orthogonal line that the viewer is looking at? Let's rotate the picture and look from the viewer's point of view.
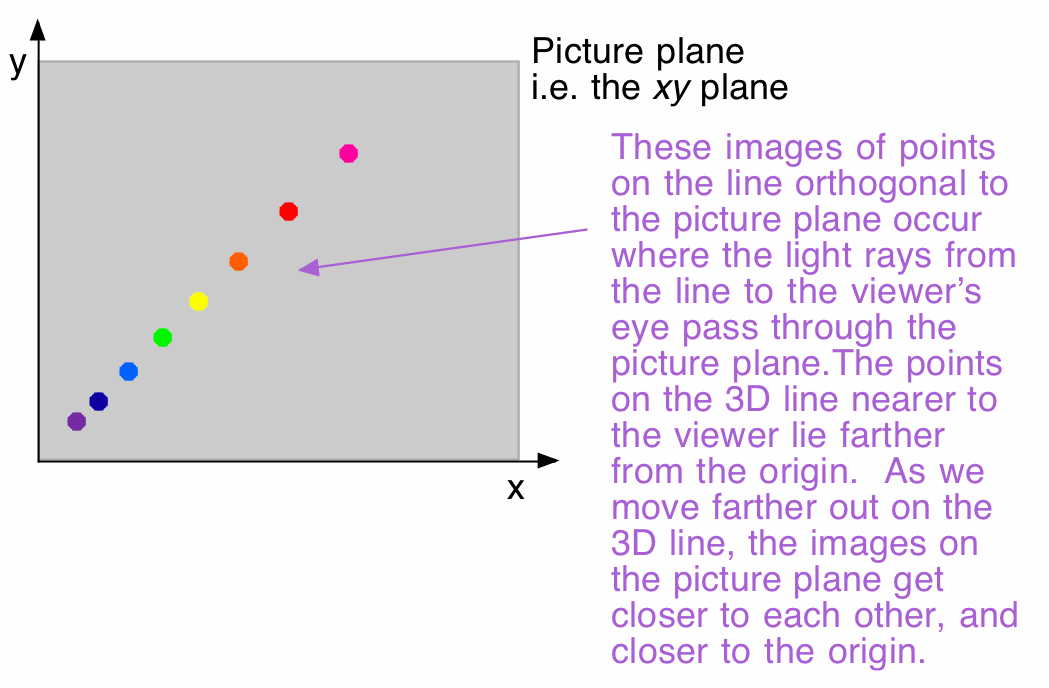
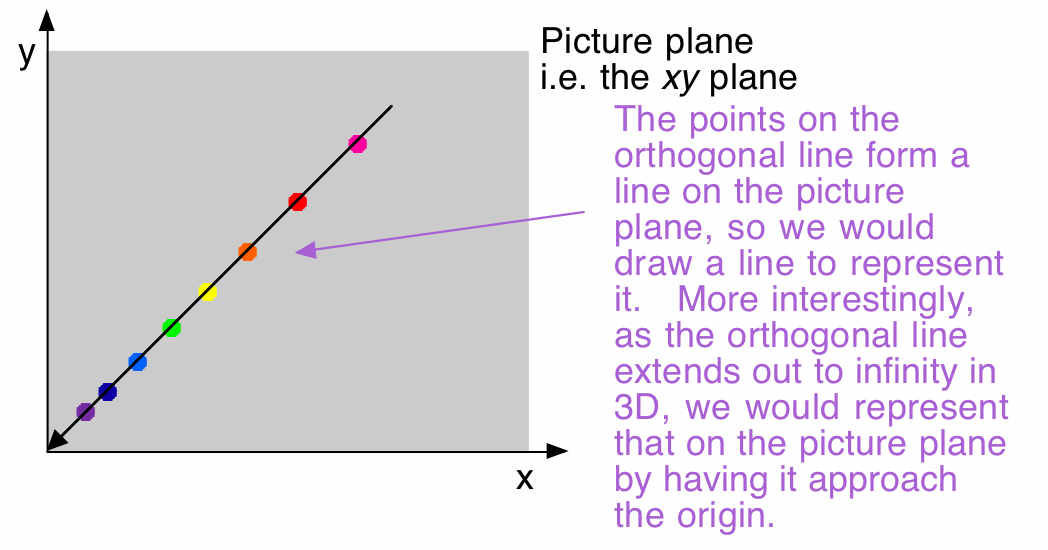
The viewer will see a line. The points on the line that are farther from the origin represent the points on the real 3D line that were closer to the viewer. As the points on the 3D line got farther and farther from the viewer, their images got closer and closer to each other and to the origin. The image of the infinitely long 3D line will stop at the origin -- it is there that the viewer's line of sight leaves the line, becoming parallel to it, and so the viewer can no longer see the line.
We call the origin the vanishing point for this infinitely long line.