Vanishing Points

Recall: Draw the perspective image of a 3D line so that its vanishing point is the point on the picture plane where the assumed viewer's line of sight that is parallel to the real-world line we're drawing the image of intersects the picture plane -- this corresponds to when the artist's assumed viewer is looking all the way to the infinite end of that line (if such a thing were possible).

The Vanishing Point Theorem
Suppose we have 2 (or more) lines in the real world that are parallel to each other, but not to the picture plane. Then their perspective images will not be parallel, but will all intersect at the same point. The point where they intersect is their vanishing point.

if our lines are orthogonal to the picture plane (parallel to the z-axis), then the vanishing point will be directly opposite the viewer's eye, at the origin.

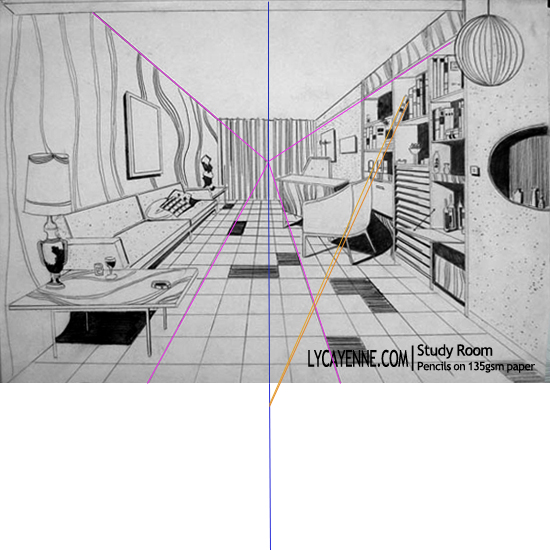
The vanishing point of all the orthogonals is called the primary vanishing point.

We call the horizontal line through the primary vanishing point the horizon line.

Since the primary vanishing point is at the origin, the horizon line corresponds to the x-axis.

If our parallel lines are still parallel to the "floor" (the xz-plane) but no longer orthogonal to the picture plane, then their shared vanishing point will no longer be at the origin, but will still be on the horizon line/x-axis.

This is because if the viewer's line of sight is parallel to the line we're looking at, the it's parallel to the xz-plane. Since the line of sight begins in the xz-plane (the viewer's eye is on the z-axis), it must stay in the xz-plane. Thus it must hit the picture plane on the x-axis somewhere.
There is no reason why any of the vanishing points needs to be on the canvas at all.

In the painting on the left, we know all of the highlighted lines are parallel to the "floor" (the xz-plane), and thus we still know they vanish on the horizon line, as we did above, even though this painting is not in one-point perspective and so we don't have a primary vanishing point. Thus a viewer can at least figure out at what level their eye should be, even if they can't tell opposite which point exactly to put their eye.

If instead of our parallel lines being parallel to the "floor" , we have parallel lines which are parallel to the "side wall" (the yz-plane), their shared vanishing point will again no longer be at the origin, but will still be on the vertical line through the primary vanishing point -- the y-axis, or what we are choosing to call the verizonline.

Next!

Back to Perspective! | Back to In Class!