A Mathematical Example of Growth at One End
Below, I illustrate an abstract process of growth at one end. Is it gnomonic? In other words, when I attach the new square to the old figure, is the resulting rectangle similar to the figure I started out with?
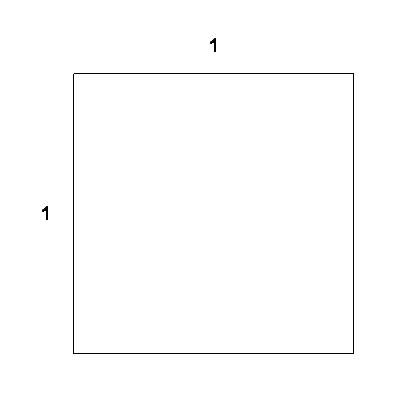 | We begin with a square of side 1. | 1 |
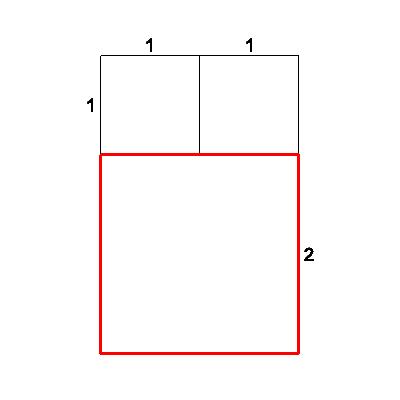
 | To this, we attach another square. In order to form a rectangle, the attachment must have side 1. Is the new figure (a 2 x 1 rectangle) similar to the old figure (a 1 x 1 square)? Obviously not. So far, our attachment does not represent a gnomon. Do notice that the ratio of corresponding sides is new short/old short=1/1=1 | 1 |
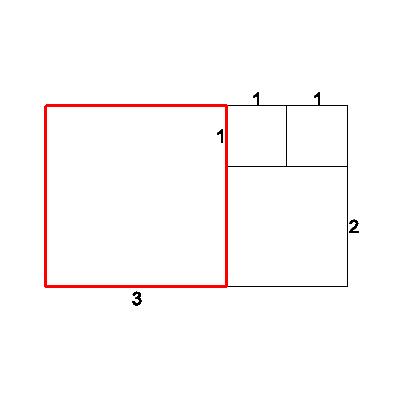
 | Again we attach a square -- to the larger side of our 2x1 rectangle -- so a 2x2 square. Is the new figure (a 3x2 rectangle) similar to the old figure (a 2 x 1 rectangle)? Again, obviously not. Notice that the ratios are closer together than they were, however: new short/old short=2/1=2 | 2 |
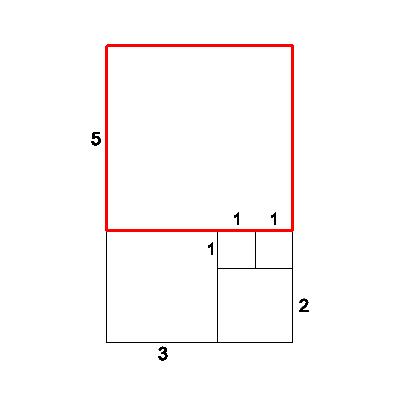
 | Attach a 3x3 square to the larger side of our 3x2 rectangle. Is the new 5x3 rectangle similar to the old 3x2 rectangle? Look at the ratios of corresponding sides: new short/old short=3/2=1.5 |
3 |
 | Continuing in the same vein, we attach a 5x5 square, forming a new 5x8 rectangle from the 3x5 rectangle. Looking at the ratios again, we observe: new short/old short=5/3=1.666666.... | 5 |
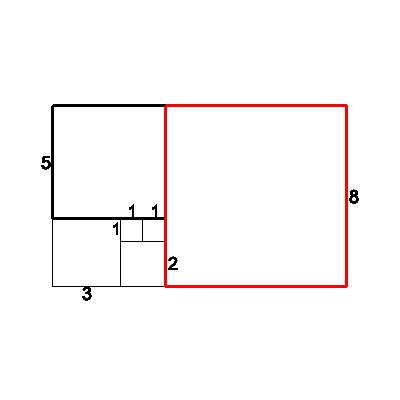 | Continuing in the same vein, we attach an 8x8 square, forming a new 8x13 rectangle from the 5x8 rectangle. Looking at the ratios again, we observe: new short/old short=8/5=1.6 | 8 |
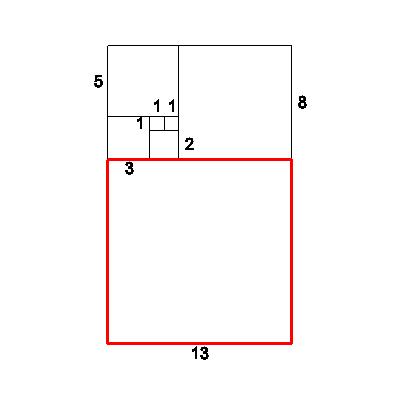 | Next, we attach a 13x13 square, forming a new 13x21 rectangle from the 8x13 rectangle. Looking at the ratios again, we observe: new short/old short=13/8=1.625 | 13 |
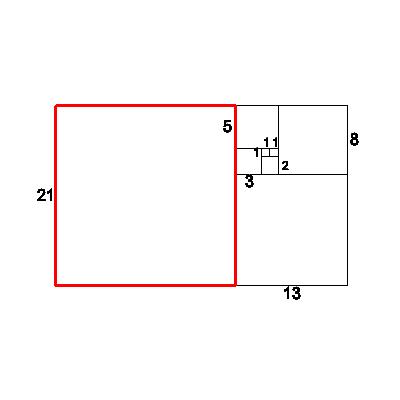 | Now attach a 21x21 square, forming a new 21x34 rectangle from the 13x21 rectangle. Looking at the ratios again, we observe: new short/old short=21/13=1.615384615 | 21 |
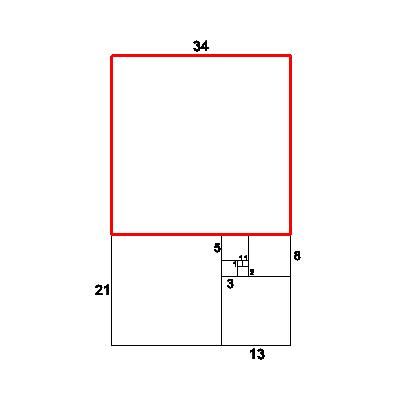 | Now attach a 34x34 square, forming a new 34x55 rectangle from the 21x34 rectangle. Looking at the ratios again, we observe: new short/old short=34/21=1.619047619 | 34 |
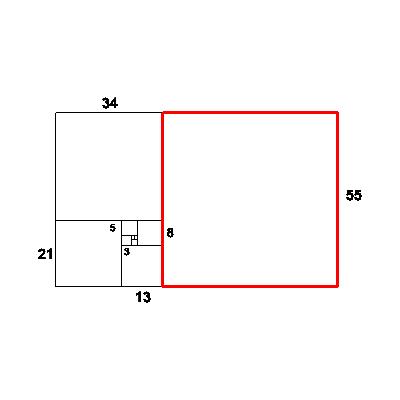 | At the next step, we add a 55x55 square, forming a new 55x89 rectangle.
new short/old short=55/34=1.617647059 | 55 |
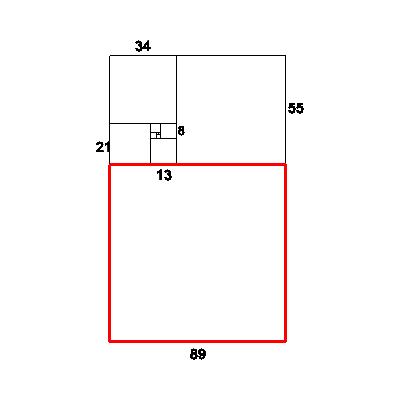 | Add an 89x89 square, to produce a 144 x 89 rectangle. Similar yet?
new short/old short=89/55=1.618181818.. | 89 |
| Add a 144 x 144 square to produce a 144 x 233 rectangle. Now the ratios of the sides is:
new short/old short=144/89=1.617977528... | 144 | |
| Add a 233 x 233 square to produce a 233x377 rectangle. Now the ratios of the sides is:
new short/old short=233/144=1.61805555... | 233 | |
| Add a 377 x 377 square to produce a 377x610 rectangle. Now the ratios of the sides is:
new short/old short=377/233=1.618025751... | 377 |
We can see that if continue in this process, we won't ever achieve actual gnomonic growth, but with each step we're getting closer and closer to the process being gnomonic growth -- that is, our old rectangle and new rectangles are now essentially similar, and will become even more and more so with each growth step.
Furthermore, notice by what factor the squares are growing each time -- the growth factor is getting closer and closer to the Golden Ratio!
If within each of these squares, we draw a quarter circle, arranging them so that each one attaches to the one that came before, we get a spiral:
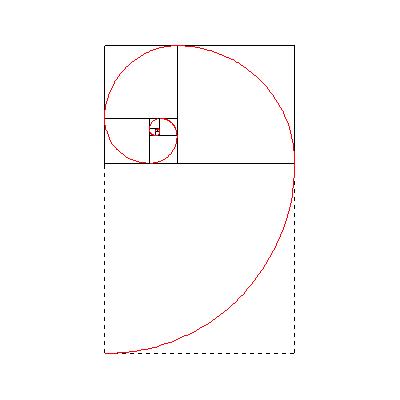
Compare this spiral to that formed by a nautilus
First intro to the Fibonacci Numbers