Be sure to check back often, because assignments may change!
(Last modified: Thursday, October 28, 2010, 11:21 AM )

All section and page numbers refer to sections from Calculus: Early Transcendental Functions, 3rd Edition, by Smith and Minton.

I'll use Maple syntax for some of the mathematical notation on this page. (Paying attention to how I type various expressions is a good way to absorb Maple notation). I will not use it when I think it will make the questions too difficult to read.

Due Friday 10/1 at 8am

Project 1 (continued)

To read: You should have read through the entire letter before lab on Thursday. Before class on Friday, re-read the letter, and review the work you did in lab on Thursday.

No Reading Questions Today

Reminder:

• Begin WW 5 and PS 5. Get an early start on it -- because of the exam, PS 5 will not be collected (WW 5 will still be due), but should be completely done by the beginning of class on Wednesday, as the material covered by PS 5 will be on the exam.

Due Monday 10/4 at 8am

Section 2.5: The Chain Rule

To read: Through Example 2.5.4. In Example 2.5.3, pay particular attention to how rewriting h(x) in various ways allows you to think of different approaches to differentiating the function.

Reading questions:

1. Consider the "simple examples" that open the section, on page 189.
   1. Why would you speculate that the derivative of (x²+1)⁴ is 4(x²+1)³(2x)?
   2. If, as the book suggests toward the bottom of page 189, we let g(x)=x²+1 and f(x)=x⁴, then what is f '(x)? f '[g(x)]? g'(x)? How are these pieces related to the conjectured derivative above?
2. When do you use the chain rule to differentiate?

Submit answers through OnCourse

Reminder:

• Spread your studying for the exam out over several days -- I know it's difficult for some people to study that way, but the material really does sink in better when you do.

Due Wednesday 10/6 at 8am

Bring Questions for Exam 1

No Reading Questions Today
Reminders:

• As you prepare for the exam, be sure to take advantage of all the Kollett Center has to offer, as well as my office hours!
• Get questions on PS 5 out of the way before class! This problem set should be finished before class, so you can be focusing on reviewing the semester to date.
• For the exam, you may have a "cheat sheet", consisting of notes handwritten by you on one side of an 8 1/2 x 11 (or smaller) piece of paper.
• You may begin taking the exam at 12:30pm Thursday.

Due Friday 10/8 at 8am

Section 2.5: The Chain Rule

To read: Review the chain rule.

No Reading Questions Today

Reminder:

• Begin WW 6 and PS 6. Note that because of October break, this WeBWork will be due on Thursday, and the problem set will be due on Friday.
• Be sure to meet frequently with your group to work on your project -- you will find that even after figuring out the mathematics of your response, writing the response is difficult and takes time and much consultation.

Due Monday 10/11 at 8am

Enjoy October Break!

Due Wednesday 10/13 at 8am

Section 2.6: Derivatives of Trigonometric Functions
Section 2.7: Derivatives of Exponential and Logarithmic Functions (for Thursday)

To read: All. In Section 2.6, pay particular attention to the clever steps in the proof of Lemma 2.6.4, and to the use of trigonometric identities and factoring in the proof of Theorem 2.6.1. In Section 2.7, pay particular attention to the way the chain rule comes into play wiht exponential functions in Examples 2.7.2 and 2.7.3. Also, just be aware that we will be seeing a slightly different proof of Theorem 2.7.3.

Reading questions:

1. What is lim _{h → 0} ^sin(h)⁄_h?
2. What is lim _{h → 0} ^(1-cos(h))⁄_h?
3. Why are the limits in the first two questions so important in this section?
4. Use the derivative of cosine and rules from Section 2.4 or 2.5 to differentiate ¹⁄_cos(x).

Submit answers through OnCourse

Reminder:

• Just a mid-semester reminder: some students feel that reading assignments are "busy work", but I have many reasons for assigning them (none of which are just to keep you busy): to ensure you have multiple exposures to the material which helps it sink in; to teach you how to actively read technical material, by example; and to give you credit for the effort you put into reading -- "free points", since I don't grade on correctness.
• Read the guidelines and the checklist before beginning to write your letter. It will not be easy to write, so leave plenty of time.
• Bring your remaining questions on PS 6 to lab on Thursday.

Due Friday 10/15 at 8am

Section 2.6 and Section 2.7

To read: Review both sections.

No Reading Questions Today

Reminder:

• (Added 10/13/10) For those of you who are taking advantage of the extra credit (and extra learning) opportunity afforded by redoing any or all problems on the exam, remember that those are due by 3:30 Friday afternoon. (Also remember, on each problem, you earn at most the difference between what you earn the second time and what you earned the first time -- so there's no point to redoing a problem you already got correct.)
• Put plenty of time and thought into writing the final drafts of the projects, which are due Monday at 4pm
• PS 7 is another group assignment. Once again, I urge you to switch partners. If you were not the primary author last time, you should be this time. As always, do not split up the problems between you.
• We will be skipping Section 2.8.

Due Monday 10/18 at 8am

Section 2.9: The Mean Value Theorem

To read: All. As the text suggests, be sure to try drawing functions where f is continuous on [a,b], differentiable on (a,b), and f(a)=f(b), but doesn't have a horizontal tangent anywhere on (a,b).

Reading questions:

1. Suppose f(x) is continuous on [a,b] and differentiable on (a,b). Does Rolle's Theorem tell you how to find the point c in (a,b) such that f '(c)=0?
2. Why do we say that Rolle's Theorem is a special case of the Mean Value Theorem?
3. In the proof of Theorem 2.9.5, why does showing that f(b)=f(a) for the arbitrary points a and b allow us to conclude that f is constant on the interval I?

Submit answers through OnCourse

Reminder:

• The project is due by 4pm Monday. Postponed until Friday Be sure to use the extra time well.

Due Wednesday 10/20 at 8am

Introduction to Chapter 3
Section 3.2: Indeterminate Forms and l'Hôpital's Rule

To read: All

Reading questions:

1. Does l'Hôpital's Rule apply to lim_{x→ ∞} ^x2⁄_e^x ? Why or why not?
2. Does l'Hôpital's Rule apply to lim _{x→ ∞} ^x2⁄ _sin(x) ? Why or why not?

Submit answers through OnCourse

Reminders:

• We are skipping Section 3.1; instead, at the end of Chapter 3, we will be doing a section outside of your book on Taylor polynomials that covers similar but even more useful ideas.
• Use the writing guide and the checklist when writing your letter to Jill.
• There will be a differentiation exam during the last 20-25 minutes of class. Practice as wide a variety of differentiation problems as you can.
• Bring your remaining questions on PS 7 to class. Be aware that because of the differentiation exam, we won't have as long to go over questions as we usually do.
• Remember to put a star next to the primary author's name.

Due Friday 10/22 at 8am

Section 3.3: Maximum and Minimum Values

To read: All

Reading questions:

1. For each of the intervals below, please answer the following question: If f is continuous on the interval, must f have an absolute maximum and an absolute minimum on that interval? If not, can it have an absolute maximum or an absolute minimum on that interval?
   1. [-5,5]
   2. (-∞, ∞)
2. Does the Extreme Value Theorem help with finding absolute extrema, when it applies?
3. Suppose that c is a critical number for f. Must f have a local extremum at x=c?

Reminders:

• The project is due by 3:00pm.
• If you need to re-take the differentiation exam, please do not put it off. And definitely do not put it off out of any sense of embarrassment or conviction that you don't want to come by my office until you can differentiate better -- many people use the differentiation exam as an opportunity to ask, practice, and improve.
• As usual, get started on the next homework assignments

Due Monday 10/25 at 8am

Section 3.4: Increasing and Decreasing Functions

To read: All. As always, pay attention to the marginal graphs, comments, and charts -- most people find the charts that help determine where a function is increasing and decreasing to be very helpful. Also play close attention to the last paragraph in Example 3.4.1, as well as the paragraph in between Example 3.4.1 and 3.4.2.

Reading questions:

1. The graph of a function f '(x) from x=-10 to x=10 is shown below. Estimate the intervals on which f is increasing. How about decreasing?
   
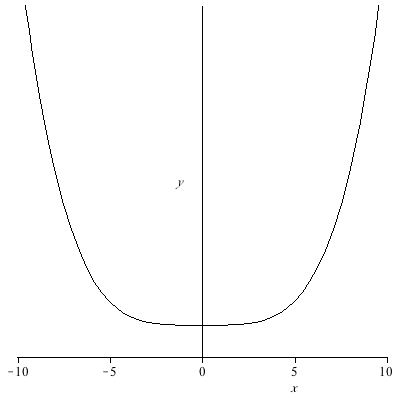
2. Use the Calculus methods from this section to determine on what intervals the function g(x), where g(x) is given below, is increasing and decreasing. g(x)=6x⁴-3x²+5000

Submit answers through OnCourse

Reminders:

• If you need to, retake the differentiation exam!

Due Wednesday 10/27 at 8am

Section 3.5: Concavity and the Second Derivative Test

To read: All. Once again, and as usual, pay attention to all marginal comments, graphs, and charts. The charts for keeping track of concavity and inflection points are just as useful as those for determining direction and extrema.

Reading questions:

1. On page 287, consider Figures 3.5.55 a and b, and 3.5.56 a and b. In figure 3.5.55a, the graph is getting steeper, while in Figure 3.5.56a, the graph is getting flatter -- yet in both cases, the authors write that the slopes of the tangent lines are increasing. Similarly, in Figure 3.5.55b, the graph is getting flatter, while in Figure 3.5.56b, the graph is getting steeper -- yet in both cases, the authors say that the slopes of the tangent lines are decreasing. What is going on here?
2. Are all points where f ''=0 or is undefined automatically inflection points?

Reminder:

• Bring questions on PS 8.
• Exam 2 will be on 11/4.
• In order to receive 100% on the differentiation exam, you must pass it by 4pm on Monday 11/1.

Due Friday 10/29 at 8am

Section 3.6: Overview of Curve-Sketching

To read: All

Reading questions:

1. What is the point of learning how to sketch curves, given how available graphing tecnology now is?
2. In Example 3.6.4,
   1. How do the authors conclude that f'(x)<0 for all x ≠ a, -1?
   2. The authors say we can disregard the factor of x² +3x+3 in the numerator of f ''(x) because it is always positive. What is one way that you can figure out that it is always positive?
   3. Why does the factor x²+3x+3 being always positive mean that we can disregard it when discussing the sign of f ''(x)?

Submit answers through OnCourse

Reminder:

• Get an early start on WW9 --as before, WW 9 will not count toward your grade, but this time I built the problems on study guide around assuming you are doing WW 9 as well.
• Again, I remind you - if you haven't already passed the Differentiation Exam, you must pass it by 4pm Monday 11/1 in order to receive 100% on it.