I'll use Maple syntax for mathematical notation on this page.
All section and page numbers refer to sections from Lay, updated 2nd edition.

Due Monday 10/1 at 8am

Introduction to Chapter 2
Section 2.1: Matrix Operations
Section 2.2 : The Inverse of a Matrix

• To read: All of the Introduction and Section 2.1, Section 2.2 through Example 4.
• Be sure to understand: In Section 2.1, the section "Matrix Multiplication" and Example 3; in Section 2.2, the statement of Theorem 5.

E-mail Subject Line: Math 221 Your Name 10/1

Reading questions:

1. If A is a 10 x 7 matrix and B is a 2 x 10 matrix, does AB exist, and if so, how many columns does it have? How about BA?
2. Give one way in which matrix multiplication differs from multiplication of real numbers.
3. Suppose A is an invertible matrix. Can Ax=b have infinitely many solutions?

Reminder:

• You will be receiving the take-home exam Monday in class. Make sure you have copies of all group homework {\em before} then, as asking for a particular homework from a colleague becomes problematical (that is, open to interpretation as being dishonourable) once you have the exam in your possession.

Due Wednesday 10/3 at 8am

Section 2.2 : The Inverse of a Matrix
Section 2.3: Characterization of Invertible Matrices

• To read: Finish Section 2.2, read all of Section 2.3.
• Be sure to understand: In Section 2.2, the statement of Theorem 7; in Section 2.3, the statement of Theorem 8.

E-mail Subject Line:<

Math 221 Your Name 10/3

Reading Questions:

1. Find the inverse of the matrix A defined as 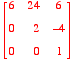. Use Maple notation to write the result.
2. Suppose A=[u, v, w] is invertible. What is span{u, v, w}?
3. In Example 2 in Section 2.3, how do we know that T maps Rⁿ onto Rⁿ?

Reminder:

• Following the honor code regarding the take home exam means not discussing the exam at all with anybody but me.
• Don't put off working on the exam. (I give you four days for a reason!)
• Come to me with questions -- but only after you really have thought about the question and looked through your book, notes, and homework for ideas!

Due Friday 10/5 at 8am

The Big Picture

• To read: Review Sections 1.7 through 2.3. (Presumably, you are anyway, for the exam)
• Be sure to understand: Try to see the big picture, the connections betweeen the ideas.

Exam 1 Due Today. No Reading Questions

Monday 10/8: Enjoy your Fall Break!

Due Wednesday 10/10 at 8am

Section 1.9: Linear Models in Business, Science, and Engineering
Section 4.9: Applications to Markov Chains

• To read: The section "Difference Equations" in Section 1.9 and all of Section 4.9.
• Be sure to understand: The section "Predicting the Distant Future" in Section 4.9

E-mail Subject Line: Math 221 Your Name 10/10

Reading questions:

1. What is the point of studying Markov chains?

Due Friday 10/12 at 8am

Section 1.9: Linear Models in Business, Science, and Engineering
Section 4.9: Applications to Markov Chains

• To read: Re-read
• Be sure to understand: Understand more deeply

E-mail Subject Line: Math 221 Your Name 10/12

Reading questions:

1. What is a steady state vector for a stochastic matrix P?
2. What is special about regular stochastic matrices?

Due Monday 10/15 at 8am

Section 2.8: Applications to Computer Graphics

• To read: Through the section "Homogeneous 3D Coordinates"
• Be sure to understand: Examples 4, 5, and 6

E-mail Subject Line: Math 221 Your Name 10/15

Reading questions:

1. What is the advantage of using homogeneous coordinates in computer graphics?

Due Wednesday 10/17 at 8am

Introduction to Chapter 3
Section 3.1: Introduction to Determinants
Section 3.2: Properties of Determinants

• To read: All
• Be sure to understand: The definition of determinant, and the statements of Theorems 3, 4, and 6

E-mail Subject Line: Math 221 Your Name 10/17

Reading questions:

1. Why do we care about finding det(A)?
2. If A=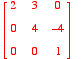, what is det(A)?

Due Friday 10/19 at 8am

The Big Picture

• To read: Review Sections 1.9, 4.9, 2.8, 3.1 and 3.2
  
• Be sure to understand: Deeper connections than you did the first time around

E-mail Subject Line: Math 221 Your Name 10/19

Reading questions:

1. Write a brief summary of Sections 3.1 and 3.2. Focus on the big ideas and the connections between them.

Due Friday 10/22 at 8am

Introduction to Chapter 4
Section 4.1: Vector Spaces and Subspaces

• To read: All
• Be sure to understand: The definition of a vector space and a subspace, Examples 4 and 8, and the statement of Theorem 1

E-mail Subject Line: Math 221 Your Name 10/22

Reading questions:

1. Is the subset of R³ consisting of all scalar multiples of the vector (5, 6, -3) a subspace of R³? Why or why not?
2. Give an example of a subset of R² that is not a subspace of R²?

Due Wednesday 10/24 at 8am

Section 4.2: Null Spaces, Column Spaces, and Linear Transformations

• To read: All
• Be sure to understand: The section "The Contrast between Nul A and Col A"

E-mail Subject Line: Math 221 Your Name 10/24

Reading questions:

1. True or False: If A is a 3 x 5 matrix, then Nul A and Col A are subspaces of R³
2. Let A=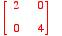. Find Nul A.

Due Friday 10/26 at 8am

Section 4.3: Linearly Independent Sets; Bases

• To read: All
• Be sure to understand: The definition of a basis, Theorem 5, and the section "Two Views of a Basis"

E-mail Subject Line: Math 221 Your Name 10/26

Reading questions:

1. Let v₁=(1,2), v₂=(3,4), and v₃=(4,6). Give a basis for H=Span{v₁, v₂, v₃}.
2. If A is a 4 x 5 matrix with three pivot positions, how many vectors does a basis for Col A contain?

Due Monday 10/29 at 8am

The Big Picture

• To read: Review Sections 4.1 through 4.3
• Be sure to understand: Get a deeper understanding of the ideas than you had before

E-mail Subject Line: Math 221 Your Name 10/29

Reading Questions:

• Write a brief summary of Sections 4.1 through 4.3. As always, focus on the big ideas and the relationship between them.

Due Wednesday 10/31 at 8am

Section 4.5

• To read: All
• Be sure to understand: Theorems 10, 11, and 12

E-mail Subject Line: Math 221 Your Name 10/31

Reading questions:

1. What is the dimension of R³? Why? Does this make sense geometrically?
2. Can there be a set of linearly independent vectors {v₁, v₂, ..., v₁} that does not span R¹²? Explain.