
Fall 2001, Math 101
I'll use Maple syntax for mathematical notation on this page.
Section 6.5: Least Squares Problems
RZ say:
BH and AJ say:
Section 6.3: Orthogonal Projections
Reading questions:
I say:
Because y=1e1+2e2+3e3, we know that the orthogonal projection of y onto the xz-plane is the vector y-hat=(1,0,3).
Note that the projection is a vector and not a scalar.
MT says:
Section 5.6: Discrete Dynamical Systems
Reading questions:
MB says:
The eigenvalues are greater than one so the
origin is a repellor.
Section 5.3: Diagonalization
Reading questions:
MT says:
JM says:
Section 5.2: The Characteristic Equation
Reading questions:
I say:
Thus det(A-(lambda)I)=(7-lambda)(1-lambda)+8, and therefore, the characteristic equation is
JL, RZ, and JA combine to say:
Characteristic equations make it so that there is only one variable in
the (A-kI)x=0 equation.
The multiplicity of an eigenvalue lambda is its multiplicity as a root of the characteristic equation.
Section 5.1: Eigenvectors and Eigenvalues
Reading questions:
RZ says:
I add:
MB says:
I add:
Section 4.6: Rank
Reading Questions:
RZ says:
GC says:
MT says:
We multiply Au and get the vector (3,
-6), which can be reduced to 3(1, -2).
(Therefore, it is true that Au=3u,), and so (1, -2) is an eigenvector and 3
is an eigenvalue.
Section 4.5
Reading questions:
MT says:
RZ says:
If you meant to have the set {v1, v2, ..., v12} then it
must span R12, because according to Theorem 12 (The Basis Theorem),
the set is automatically a basis for
R12, which means that the set spans R12.
Section 4.3: Linearly Independent Sets; Bases
Reading questions:
I say:
Thus we can span the same space with just v1 and v2. Now the question is, can we eliminate another one?
When you're only dealing with two vectors, the only way they can be linearly dependent is if one is a multiple of the other. Since that is not the case here, a basis for H is {v1, v2}.
MT says:
Section 4.2: Null Spaces, Column Spaces, and Linear Transformations
Reading questions:
Introduction to Chapter 4
Reading questions:
SB says:
RZ says:
Introduction to Chapter 3
Reading questions:
MT says:
SB says:
Section 2.8: Applications to Computer Graphics
Reading questions:
GC says
Section 1.9: Linear Models in Business, Science, and Engineering
Reading questions:
JM says
SB says:
Section 1.9: Linear Models in Business, Science, and Engineering
Reading questions:
MB says:
Section 2.2 : The Inverse of a Matrix
Reading Questions:
SB says:
æææThis was attained by (augmenting) matrix A with the Identity matrix as shown in example 7 of Section 2.2, and row reducing the far left side, until the identity matrix could be seen in the place of where matrix A was. æThat is, reducing it to reduced echelon form on the far left.
MT says:
Introduction to Chapter 2
Reading questions:
GC says:
However, BA does
exist, and by definition, it has 7 columns.
JM says:
BH says:
Section 1.8: The Matrix of a Linear Transformation
Reading questions:
BH says:
Section 1.8: The Matrix of a Linear Transformation
Reading questions:
SB says:
Therefore A = matrix( [ [cos(pi/4), -sin(pi/4)], [ sin(pi/4) , cos(pi/4)] ¾
RZ says:
Section 1.7: Introduction to Linear Transformations
Reading Questions:
MB says:
Hence T fails our first criterion, and so it's not a linear transformation.
JL says:
Section 1.7: Introduction to Linear Transformations
Reading questions:
JL says (more or less)
Therefore T(-4,10)=(46,-58).
The Big Picture
Reading questions:
Linear Independence
Reading questions:
GC says:
I say:
Another way to say the same thing:
So the only way the non-homogeneous equation can have an infinite number of solutions is if the homogeneous equation also has an infinite number of solutions.
JL says:
RZ says:
Section 1.5: Solution Sets of Linear Systems
Reading questions:
MB says:
JM adds:
JL says
Section 1.4: The Matrx Equation Ax=b
Reading questions:
I say:
Section 1.3 : Vector Equations
Reading questions:
This is the same as the system
From this we can immediately see that x_1=9 and x_2=1/3.
Thus y=9u+(1/3)v.
guidelines for submitting reading assignments
Reading questions:
MT says:
MB says:
SB says:
PS adds:
All section and page numbers refer to sections from Lay, Updated 2nd Edition.

Reading questions:
The point of this section is to find a way to best approximate Ax=b when
it has no solution. We are able to do this using the general least-spuares
problem. This is a way of making the space between b and Ax the smallest.
Every system Ax=b has at least one least-squares solution.
The solution is not necessarily unique, because Theorem 14 says the solution is unique only if the columns of A are linearly independent.

Let y=(1, 2, 3) in R3 and let W be the xz-plane.
We know how to project onto coordinate axes already, we don't need anything fancy for this.
There is no point in W that is closer to y than the orthogonal projection
of it. This is justified by the Best Approximation Theorem which says that
||y-^y|| < ||y-v|| for all v in W distinct from ^y.

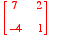 . Determine whether the origin is an attractor, a repellor, or a saddle point for solutions to
xk+1=Axk.
. Determine whether the origin is an attractor, a repellor, or a saddle point for solutions to
xk+1=Axk.
(The characteristic equation for A is)
h^2 - 8h + 15 = 0.
So h = 5,3.

Diagonalization allows us to easily find A^k, no matter what the value of
k is.
Yes, A is diagonalizable because an n x n matrix with n distinct eigenvalues is diagonalizable.æ

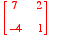 . Find the characteristic equation of A.
. Find the characteristic equation of A.
The characteristic equation is det(A-(lambda)I)=0.
A-(lambda)I has 7-lambda and 1-lambda on the diagonal, and is otherwise unchanged.
(7-lambda)(1-lambda)+8=0.
They are related because lambda is an eigenvalue of an
n X n matrix A if and only if lambda satisfies the
characteristic equation det(A- lambda *I) =0.

Suppose A is a 3 x 3 matrix with eigenvalues 1, 2, and 5.
The dimension of Nul(A) is 0 becasue of the Invertible Matrix Theorem.
A is a square matrix and 0 is not an eigenvalue. That means that A is invertible by the final statement of the invertible matrix theorem. Hence A has a pivot in every column. Since dim(Nul(A))=the number of free variables, dim(Nul(A))=0.
The dimension of the eigenspace of A is 3.
For each eigenvalue, there exists an eigenvector. Since the eigenvalues are distinct, Theorem 2 tells us that these three eigenvectors are linearly independent. That meanst that dim(eigenspace(A)) is at least 3. But since the eigenvectors are in R^3, the dimension of the eigenspace must be no more than 3. Hence the dimension of the eigenspace is exactly 3. -->

Introduction to Chapter 5
Section 5.1: Eigenvectors and Eigenvalues
The dimension of NulA when A is a 4x7 matrix with 3 pivots is 4 because
the dimension of NulA is the number of free variables in a matrix. So this
means if A has 3 pivots then there must be 4 columns without pivots making
them free variables.
The dimension of Nul A is four. By Theorem 13, the number of columns in a
matrix equals the number of pivots plus the dimension of Nul A. 3+4=7
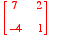 . Verify that (1, -2) is an eigenvector of A with corresponding eigenvalue 3.
. Verify that (1, -2) is an eigenvector of A with corresponding eigenvalue 3.
A= [(7, 2)], [(-4,1)] and u= (1, -2).

Seeing as how the basis for Rn has n vectors, the dimension of Rn must
be n, and therefore the dimension of R3 is 3. This makes sense geometrically
because R3 is the 3rd dimension, go figure!
JL adds:
Of course this makes geometric sense
because there are three different direction sets.
This question does not make sence to me but I might have missed something
in the reading.

Since v3=v1+v2, v3 is a linear combination of v1 and v2, and so is redundant.
According to theorem 6, the pivot columns of a matrix A form a basis for
Col A. A is a 4x5 matrix with 3 pivot positions so three vectors form a
basis for ColA.

GC says:
False. In this case, Nul A is a subspace of R5, and Col A is a subspace of
R3.
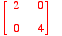 . Find Nul A.
. Find Nul A.
Combining the answers of JM and RZ:
2x1=0, 4x2=0
=> Nul A is {(0,0)}

Section 4.1: Vector Spaces and Subspaces
The subset of R3 that consists of the all the scalar multiples of the vector (5, 6, -3) is a subspace of R3 because it passes through the zero vector and it is closed under both vector multiplication and addition.
An example of a subset of R2 that is not a a subspace of R2 is a line
that does not go through (0,0).

Section 3.1: Introduction to Determinants
Section 3.2: Properties of Determinants
A determinant can give us formulas for the volume of different polyhedra.
They also give us information about matrices, information that is very useful in
linear algebra.
MB adds:
If det(A) does not equal zero and is a square matrix, then it is invertible.
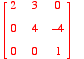 , what is det(A)?
, what is det(A)?
A cofactor expansion down the first column will make
detA=2*matrix( [ [ 4, -4], [0, 1] ]) = [=2*(4*1-(-4)*0) ] = 2*4=8

Using homogeneous coordinates is advantageous because it allows the
mathematician to use a matrix to represent a translation.
SB adds:
This
is especially useful in biology where biologists will use computer graphics
to similate a protein. The visualizing of potential chemical reactions and
changes in view can be done by using homogeneous coordinates.

Section 4.9: Applications to Markov Chains
A steady state vector for a stochastic matrix P is a probability vector such that Pq=q.
Each regular
Stochastic Matrix has a steady state vector.

Section 4.9: Applications to Markov Chains
The point of studying Markov chains is to take current trends of a specific
situation and use this to predict what will happen in the future.
MT says:
Markov chains are a way for the Linear Algebra we have been doing to be
applied to everyday situations. The way that they are set up enables us to
predict certain outcomes with specific results. If we know what x0 is, then the
nature of the chain allows us to find xk.
JL says:
The point in studying Markov chains is that they are used in many
fields. The examples from the book are biology, business,
chemistry, engineering, and physics. They are good at representing
the data of an experiment or measurement.

Section 2.3: Characterization of Invertible Matrices
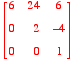 . Use Maple notation to write the result.
. Use Maple notation to write the result.
The inverse of matrix A is
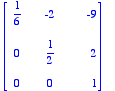
GC says:
The span of {u, v, w} is R3, according to Theorem 8.
I add:
This question is so simply asked, and yet it is surprisingly layered.
Since A is invertible, we know it is square. Since there are 3 columns, there must be 3 rows, and hence u, v, and w are all in R3. Also because A is invertible,we know that there's a pivot in every row. Thus we know that Span(u,v,w)=R3.
The Invertible Matrix Theorem points out that either all of its statements are
true or all of it's statements are false. So if A is invertible, then by the IMT,
the linear transformation T maps Rn onto Rn
I add:
To understand why this is true, we can go through some of the logic:
T is one-to-one, so the columns of the associated matrix A are linearly independent, and so A has a pivot in every column. Because T goes from R^n, A has n columns and so A has n pivots. But since T goes to R^n, A also has n rows, and so there's a pivot in every row and thus T is onto.

Section 2.1: Matrix Operations
Section 2.2 : The Inverse of a Matrix
AB does not exist, because the 7 columns of A do not match the 2 rows of B,
and it is impossible to multiply the two matrices together.
Matrix multiplication differs from multiplication of real numbers in that the cancellation laws do not hold true, for example, if AB=AC, B=C may not be true.
RZ adds:
(Another) way that matrix multipllication differs from multiplication of real numbers is that it is not commutative: AB does not always equal BA.
JL finishes with:
(Finally), multiplying matrices is different then multiplying regular
numbers because with matrices, it may be possible to multiply x by y but
not y by x, where as with real numbers, it doesn't matter which order
you put them in.
No, it does not have an infinite number of solutions. It has the unique solution
x=A-1 b, by
theorem 5.

Let T:R5 --> R3 be a linear transformation with standard matrix A, where A has three pivots.
T is not one-to-one, because of the existence of free variables. By
definition, T is one to one only if each b in Rm has either a unique solution (to T(x)=b) or
none at all.
Since there is a pivot in evey row, A spans R^m which makes T onto,
because of theorem 12.

matrix( [ [1], [ 0] ]) rotates onto matrix([ [cos(pi/4)] , [sin(pi/4) ] ]).
matrix( [ [0], [ 1] ]) rotates onto matrix([ [-sin(pi/4)], [cos(pi/4) ] ]).
Matrix([[2, 0], [0, 1]]) is the matrix A for the linear transformation T:
R2--> R2 that expands horizontally by a factor of 2.

<0L>
T does not appear to be a linear transformation because it doesn't preserve
the operations of vector addition and scalar multiplication.
I add:
In order to be linear, we need that T(u+v)=T(u)+T(v) and that T(ru)=rT(u).
T(u+v)=T(u1+v1, u2+v2)
=( u2+v2-3, 4(u1+v1)+10)
= (u2-3, 4u1+10)+(v2,4v1)
=T(u)+some other stuff that's not T(v)
A must have five columns for Ax to be defined, and A must have
three rows for the codomain of T to be R^3.

Let A be the matrix
![]() , and let T:R2 --> R2 be defined by T(x)=Ax.
, and let T:R2 --> R2 be defined by T(x)=Ax.
(-4 x 1) + (10 x 5)=46,
(-4 x 7) + (10 x -3) = -58
SB says (more or less):
 .
.
Replace Row 2 by -7(Row1)+ (Row2), to get
![]() .
.
Since we do not have a situation that equates some non-zero number to zero
(i.e. T(4, -2) is consistent), (4, -2) is within the range of T.

I am not going to display these because none are more right than others -- the point of these reading questions (they'll pop up again) is first of all to encourage you to look for the big picture every now and then, and second of all to give you practice writing synopses, because the ability to pick out a few important points and connect them is both important and difficult.

No, because for a linear independence to exist, the equation Ax=0 must have
only the trivial solution.
The only way Ax=b can have infinitely many solutions is if A has a free variable, in which case Ax=0 also has infinitely many solutions, and so we're back in the situation of #1. Hence the columns again can not be linearly independent.
We found in Section 1.5 that the general solution to a consistent system Ax=b has the form
Since there would be 3 vectors and only two equations to work
with, there would be a free variable which would mean that R2 can not
be linearly independent.
A set of 3 vectors in R2 cannot be linearly independent because one of the 3 will be in the span of the other 2 making it not linearly independent.

A homogenous system of equations is one that can be written in the form Ax=0
and nonhomogenous systems are of the form Ax = b with b not 0.
A homogeneous system of equations ... always has at least one solution.
I add:
Non-homogeneous systems may have no solutions (if the system is inconsistent), a unique solution (corresponding to the homogeneous system having only the trivial solution), or infinitely many solutions (corresponding to the homogeneous system having infinitely many solutions, i.e. when A has at least one free variable.)
Ax=b would have infinite solutions because since there is at
least one ... answer and there is a free variable, there would be
an infinite amount of solutions.

MT says:
According to Theorem 4, a matrix with four columns, such as this one must have
at least 4 pivot points, not three like the problem suggests.
![]()
To merely simplify it, rather than actually calculating it, we can use Theorem 5, which tells us that
Thus the above simplifies to matrix[( (7,3),(-1,4) )]*( (-5,4)+(6,3) ), or
To then go ahead and calculate it, I'd get:
(7*1+3*7, -1*1+4*7)=(28,27).

If y is a linear combination of u and v, that means that I can get y by adding scalar multiples of u and v:
0x1+12x2=4
1x2+0x2=9
0x1+9x2=3
Span{u,v} is the set of all linear combinations of u and v.
Thus Span{u,v} consists of all vectors of the form
au+bv=(a,0,0)+(0,b,0)=(a,b,0)
where a, b can be any real numbers.
Thus Span{u,v} is the xy-plane in R3.

suggestions for reading a math text
course policies
syllabus
Introduction to Chapter 1
Section 1.1: Systems of Linear Equations
Section 1.2: Row Reduction and Echelon Form
Let A be the matrix

The matrix A is in echelon form because all nonzero rows are above the zero
rows, each leading entry is to the right of the leading entry above it, and all
entries stacked below a leading entry are zero.
The values in the pivot positions of A are 5, 7, and 4.
A is not consistent because in the last row it states that 0=4. This
does not make sense, making A inconsistent.
Because the rightmost column of the matrix is a a pivot column the
matrix is inconsistent.
Janice Sklensky
Wheaton College
Department of Mathematics and Computer Science
Science Center, Room 109
Norton, Massachusetts 02766-0930
TEL (508) 286-3973
FAX (508) 285-8278
jsklensk@acunix.wheatonma.edu
Back to: Linear Algebra | My Homepage | Math and CS