Be sure to check back often, because assignments may change!
(Last modified: Thursday, April 17, 2008, 11:20 AM )

I'll use Maple syntax for mathematical notation on this page.
All section and page numbers refer to sections from Smith & Minton's Multivariable Calculus, 3rd edition.

Due Wednesday 4/2 at 9am

Section 13.1: Double Integrals (continued)

• To read: Re-read the section. Pay careful attention to Example 1.7 -- I know it's at the end of a long section, but it is crucial.

E-mail Subject Line: Math 236 Your Name 4/2

Reading questions:
In the double integral ∫∫_R f(x,y)dA,

1. What does dA represent?
2. Do the two integral signs go together -- that is, are they, in a sense, a new symbol? Or do they represent first one integral and then another?

Due Friday 4/4 at 9am

13.2: Area, Volume, and Center of Mass

• To read: All

E-mail Subject Line: Math 236 Your Name 4/4

Reading questions:

1. If R is the circle of radius 3 centered at the point (5,1), what is ∫∫_R dA? (You should be able to do this without setting up any iterated integral)
2. Is M_y used to compute the x- or the y- coordinate of the center of mass? And in a related question -- why do you think it's called M_y?

Reminders:

• You don't have a problem set due next week because of the exam, but you still should do the problems from Section 13.1 and 13.3 before the exam.

Due Monday 4/7 at 9am

Section 9.4: Polar Coordinates
Section 13.3: Double Integrals in Polar Coordinates

• To read: All of Section 9.4; through Example 3.2 in Section 13.3.

E-mail Subject Line: Math 236 Your Name 4/7

Reading questions:

1. Find one polar coordinate representation for the rectangular point (5,-2).
2. Find rectangular coordinates for the polar point (1,Pi/3).
3. The graphs of (a) r=sin(7θ) and of (b) r=sin(7θ)+5 are shown below. Match the functions to the graphs.

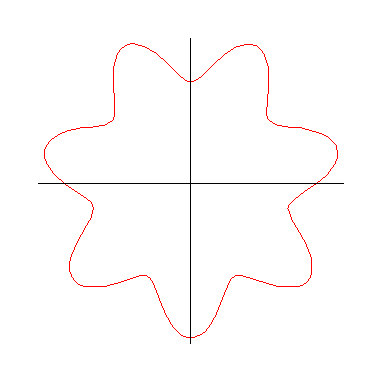
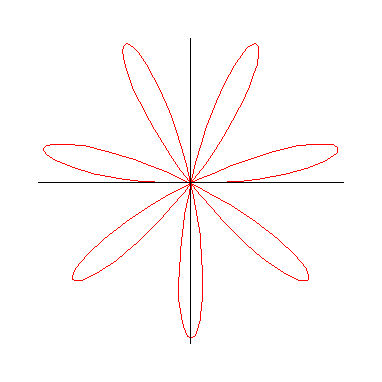
• polarplot(sin(7*theta),theta=0..Pi);
• polarplot(sin(7*theta)+5, theta=0..2*Pi);

Due Wednesday 4/9 at 9am

Exam 2 - In Class Portion

No Reading Questions Today!

Due Friday 4/11 at 9am

Section 13.3: Double Integrals in Polar Coordinates

• To read: Finish

E-mail Subject Line: Math 236 Your Name 4/11

Reading questions:

1. Why might we want to convert a double integral from rectangular coordinates to polar coordinates?
2. When we use iterated integrals to evaluate an integral in polar coordinates, what is dA?

Due Monday 4/14 at 9am

Section 13.4: Surface Area

• To read: All

E-mail Subject Line: Math 236 Your Name 4/14

Reading questions:

1. Give a real-world example where you would want to compute the surface area.
2. After partitioning the region R, what objects are used to approximate the surface area over each subregion R_i?
3. Where does the cross-product come in?
4. What formula from earlier in the semester does the formula for surface area remind you of? Why might these two quantities have similar formulae?

Reminders:

• The take-home portion of Exam 2 is due at 4:30 Monday.

Due Wednesday 4/16 at 9am

Section 13.5: Triple Integrals

• To read: All

E-mail Subject Line: Math 236 Your Name 4/16

Reading questions:

1. Why might you need to compute a triple integral?
2. What is often the hardest part of calculating a triple integral?

Reminder:

• PS 9 is again a group assignment. Switch partners, don't split the problems up, and put a star next to the primary author's name.

Due Friday 4/18 at 9am

Section 14.1: Vector Fields

• To read: All

E-mail Subject Line: Math 236 Your Name 4/18

Reading questions:

1. On page 1118, figures 14.3(a) and 14.3(b) are both representations of the vector field H(x,y)=<y,-x>, yet they look very different. Based on the definition of a vector field, which of these two graphs do you think most correctly shows the vector field? Which one do you think gives you the best feel for the behavior of the vector field?
2. Suppose the vector field shown below represents the flow of a small portion of a river, and suppose a leaf were to fall into the water at the point (-2,2). Describe the movement of the leaf.
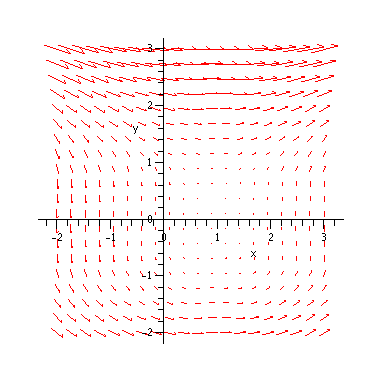
   fieldplot(f(x,y), x=-2..3, y=-2..3, fieldstrength=maximal(2),color=red);

3. Compare this behavior with the path the leaf would follow if it fell in at the point (-2,2.5) instead.

Due Monday 4/21 at 9am

Section 14.2: Line Integrals

• To read: Through Theorem 2.3, top of page 1136.

E-mail Subject Line: Math 236 Your Name 4/21

Reading questions:

1. Give two different uses for line integrals with respect to arc length.
2. If you're evaluating a line integral with respect to arclength, does the orientation of the curve matter? If so, what difference does orientation make?

Reminders:

• Your individual project is due Friday -- you should be entering the final stages!

Due Wednesday 4/23 at 9am

Section 14.2: Line Integrals (continued)

• To read: Finish

E-mail Subject Line: Math 236 Your Name 4/23

Reading questions:

1. Give at least one use for component-wise line integrals.
2. If you're evaluating a line integral with respect to any of the axes, does orientation matter? If so, what difference does orientation make?

Due Friday 4/25 at 9am

Section 14.3: Independence of Path and Conservative Vector Fields

• To read: All

E-mail Subject Line: Math 236 Your Name 4/25

Reading questions:

1. Why are conservative vector fields so helpful when evaluating line integrals?
2. Why is Theorem 3.2 called the Fundamental Theorem for line integrals?

Reminders:

• The project is due by 3pm Friday.

Due Monday 4/28 at 9am

Section 14.4: Green's Theorem

• To read: All

E-mail Subject Line: Math 236 Your Name 4/28

Reading questions:

1. What surprises you about Green's Theorem?
2. Give an example of a region R in the plane where Green's Theorem does not hold.

Due Wednesday 4/30 at 9am

Section 14.4: Green's Theorem (continued)

• To read: Re-read the section

No reading questions today

Due Friday 5/2 at 9am

Final - In Class Portion

No reading questions today