Be sure to check back often, because assignments may change!
(Last modified: Monday, March 29, 2010, 9:52 AM )

I'll use Maple syntax for mathematical notation on this page.
All section and page numbers refer to sections from Smith & Minton's Multivariable Calculus, 3rd edition.

Monday 3/1 at 9am

Section 11.6: Parametric Surfaces

• To read: All. I'd again suggest reading while sitting by a computer with Maple, so that you can follow along with their comments about what things look like when graphed various ways, with the help of your cheat sheet. And again, if you don't feel like you know enough Maple to do this, please come see me!
  When you get to the discussion before Example 6.4, don't panic that you haven't seen polar coordinates much: all you need to know is what they tell you.

E-mail Subject Line: Math 236 Your Name 3/1

Reading questions:

1. Following a process similar to that in Example 1 (not using Maple to graph), identify the surface defined by the parametric equations x=2cos(u)sin(v), y=2sin(u)sin(v), z=6cos(v). (You might want to review the generic equations for quadric surfaces given in Section 10.6).
2. In Example 6.3, what might make you think to use cosh(u) and sinh(u) in the parametric equations for x and y? That is, what property that's useful in this situation do they have?

Reminders:

• Please come clear up any lingering difficulties before the test Wednesday.
• Laptops with Maple will be useful again today.

Due Wednesday 3/3 at 9am

Exam 1 (in-class portion)- No new reading!

Due Friday 3/5 at 9am

Section 12.1: Functions of Several Variables

• To read: Up through middle of page 925. This is another section where reading where you have access to Maple would not be a bad idea. When you get to example 1.6, try to figure out as much as you can about which functions go with which graphs before you read the solution; when you do read the solution, do so extremely carefully.

E-mail Subject Line: Math 236 Your Name 3/5

Reading questions:

1. Below are the graphs of 4 surfaces. 2 of them are the graphs of the functions f₁(x,y)=[(x²+y²)-2]³ and f₂(x,y)=y²sin(x). Match the functions with their graphs.

   (a)	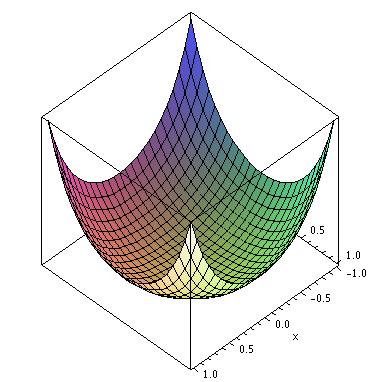	(b)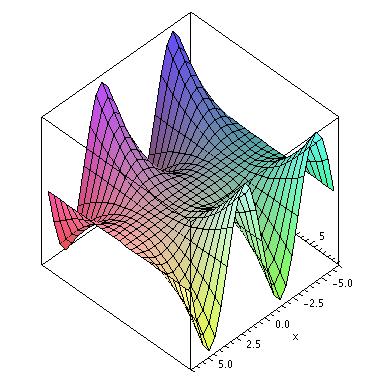
   (c)	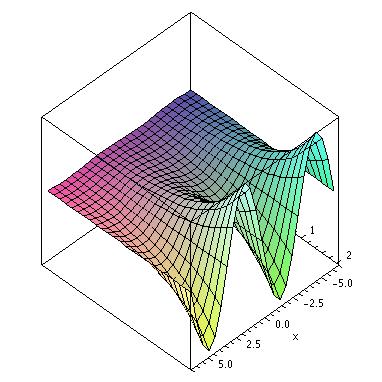	(d)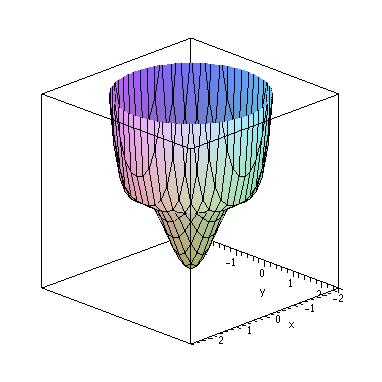

Reminders:

• Of course, there is no problem set due this week; instead make sure you work steadily at the take-home portion of your exam.
• Laptops with Maple will once again be helpful.

Due Monday 3/8 at 9am

Section 12.1: Functions of Several Variables (continued)

• To read: Finish. Pay particular attention to the definition of level curves and contour plots.

E-mail Subject Line: Math 236 Your Name 3/8

Reading questions:

1. Give the equations of two level curves for the function f(x,y)=x²/4+y²/9. What will these level curves look like?
2. Below is a contourplot for the function sin^2(x)+cos^2(y). Roughly where does it have local extrema? How can you tell?
   
   
   (I used the Maple command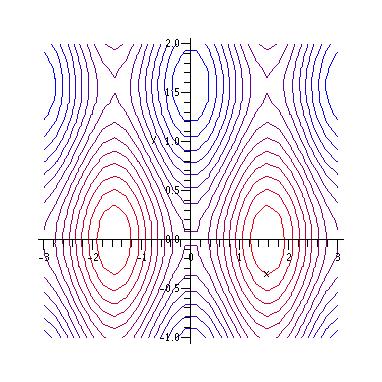
   contourplot((sin(x))^2+(cos(y))^2,x=-3..3, y=-1..2, contours=15, coloring=[blue,red]);
   to create this graph. The "coloring=" option allows you to specify which color will be associated with the lowest contours (blue) and which will be associated with the highest (red). )

Reminders:

• The take-home portion of Exam 1 is due Monday at 4:00 (which is why I'm not having you read Section 12.2 yet.)
• PS 5 is again a group assignment. Once again, switch to all new partner(s). As always, don't split problems up between you.

Wednesday 3/10 at 9am

Section 12.2: Limits and Continuity

• To read: All. Many (most?) of you will have not seen the formal definition of limit (the epsilon-delta definition) for functions of one variable. Don't worry about it. Focus on understanding the idea behind the epsilons and deltas, and what it means graphically.

E-mail Subject Line: Math 236 Your Name 3/10

Reading questions:

1. Consider f(x,y)=3x² /(x²+y²). We want to see what we can say about lim_{(x,y) -> (0,0)} f(x,y).

   (a) Find the limit along the path x=0. That is, find lim_(0,y)->(0,0) f(0,y).
   (b) Find the limit along the path y=0. That is, find lim_{(x,0) -> (0,0)} f(x,0).
   (c) What -- if anything -- can you conclude from your results?

2. What is the point of Example 2.5?
3. Why do you suppose we're studying limits now?

Reminders:

• Read about the two options for the individual project; pay attention to the various due dates -- the first one is Friday! Start thinking about which one you'd like to do.

Due Friday 3/12 at 9am

Section 12.3: Partial Derivatives

• To read: All

E-mail Subject Line: Math 236 Your Name 3/12

Reading questions:

1. For a function z=f(x,y), what information does f_y(1,2) give you?
2. For f(x,y)=ye^xy, find f_x(x,y).
3. How many second-order partial derivatives does a function f(x,y,z) have?

Reminders:

• Star the primary author's name on PS 5.
• If you haven't yet, e-mail me by Friday at 3pm to let me know which project option you're choosing.
• The reason I'm having you read all of Section 12.3 for Friday is so that you don't have to do any new reading, just some reviewing, for the Monday after break.

Monday 3/15 through Friday 3/19

Enjoy your spring break!

Due Monday 3/22 at 9am

Review Sections 12.1-12.3

• To read: Re-read these three sections.

No Reading Questions today!

Reminders:

• Get started on the project. The first substantive deadline is this Friday.

Due Wednesday 3/24 at 9am

12.4: Tangent Planes and Linear Approximations

• To read: All. Don't obsess too much over the details of the section on Increments and Differentials, but do read it, as it leads to the definition of what we mean by being differentiable at the point (a,b).

E-mail Subject Line: Math 236 Your Name 3/24

Reading questions:

1. If f(x,y) is a well-behaved function and has a local maximum at (a,b), what can you say about the linear approximation to f(x,y) at (a,b)?
2. Let L(x,y) be the linear approximation of f(x,y) at (a,b). What graphical properties of the surface z=f(x,y) would make L(x,y) particularly accurate? particularly inaccurate?
3. Let f(x,y)=xy^2. Find a vector normal to the plane tangent to z=f(x,y) at the point (2,3,18).

Due Friday 3/26 at 9am

Section 12.5: The Chain Rule

• To read: All.

E-mail Subject Line: Math 236 Your Name 3/26

Reading questions:

Suppose that w=f(x,y,z) and that x,y, and z are all functions of r,s, and t.
1. How many partial derivatives do you need to calculate to determine ∂w/∂t? (Using a tree diagram may prove useful.)
2. What is the expression for ∂w/∂t?

Reminders:

• Turn in the first stage of the project by 3pm.

Due Monday 3/29 at 9am

Section 12.6: The Gradient and Directional Derivatives

• To read: Read through Example 6.5 (page 989)

E-mail Subject Line: Math 236 Your Name 3/29

Reading questions:

1. In order to find D_uf(a,b), what must be true about our choice of u?

Due Wednesday 3/31 at 9am

Section 12.6: The Gradient and Directional Derivatives (continued)

• To read: Finish the section

Reading questions:

1. What type of quantity is the gradient of f? If we have z=f(x,y) is a surface in 3 dimensions, then what dimension does the gradient live in?
2. For f(x,y)=x^2y-4y^3,
   

   (a) Compute D_uf(2,1) for u=<-3/5,4/5>.
   (b) Compute the gradient of f(x,y)

3. Toward the top of page 988, the book says:

   ..notice that a zero directional derivative at a point indicates that u is tangent to a level curve.

   Why is this true?
4. What information does the gradient give you about f(x,y)?

Reminders:

• PS 7 is again a group assignment. As always, switch partners, don't divide the problems up, and put a star next to the primary author's name.