And still more pondering
What about lines that are neither orthogonal to the picture plane nor parallel to it? Do they have vanishing points, and if so, where?
Partial Side View (so you can see all three axes)
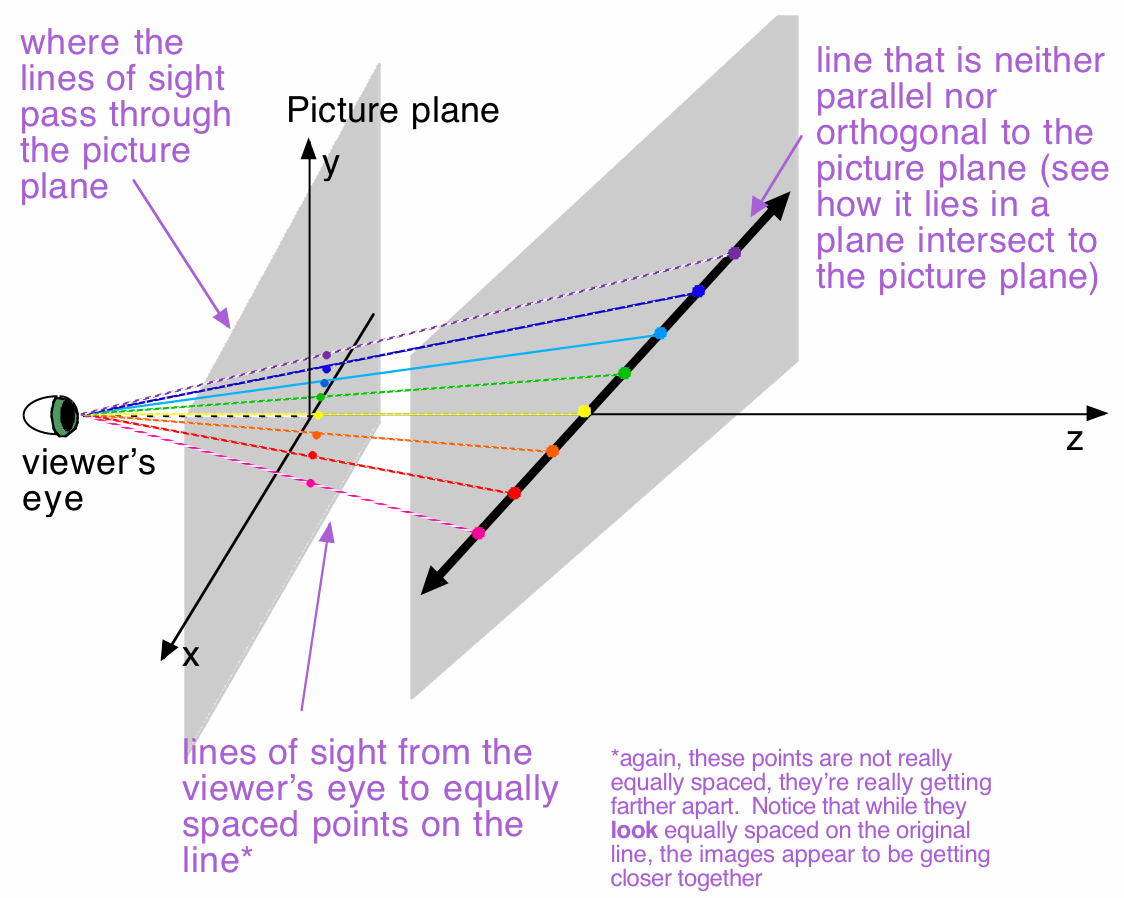
Straight-on Side View (so we can't see the x-axis)
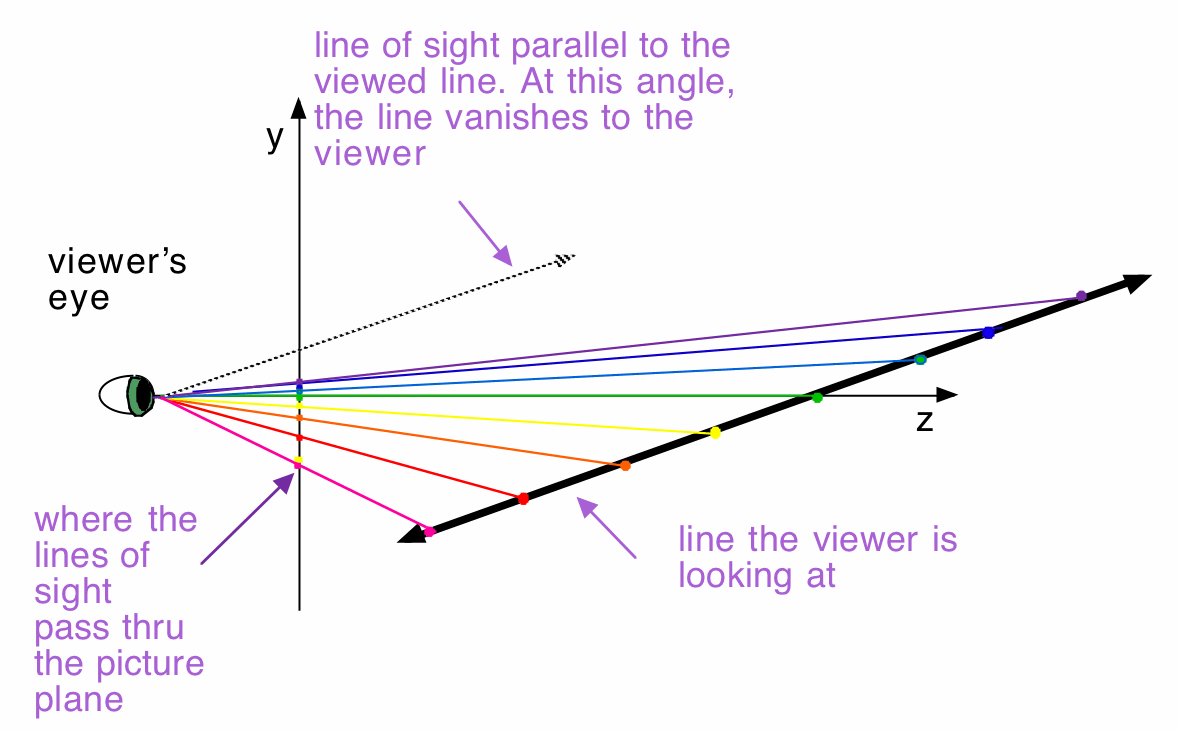
Here, we can clearly see that the y-coordinates of the perspective images of points that are equally spaced on the 3D line get closer and closer together the farther out on the line the viewer looks. Eventually, when the line of sight becomes parallel to the 3D line, the line will vanish.
Straight-on Top View (so we can't see the y-axis)
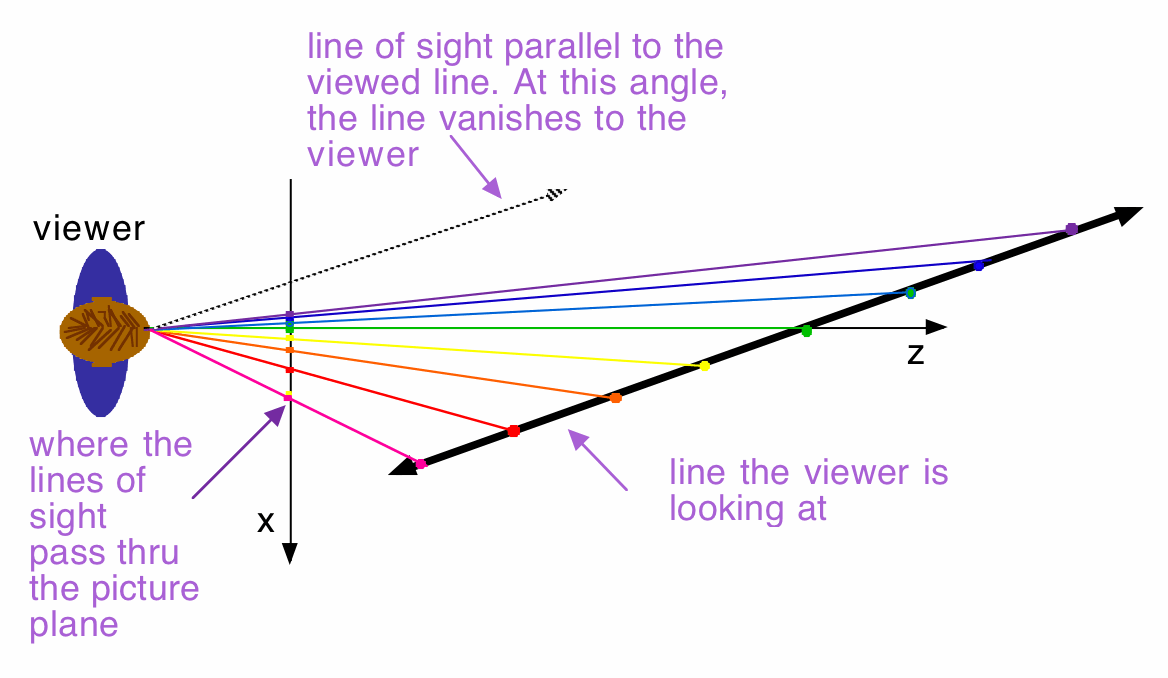
And here, we can see that the same holds true for the x-coordinates of the perspective images.
Front View - what the viewer sees
Let's again rotate around to see what the viewer sees:
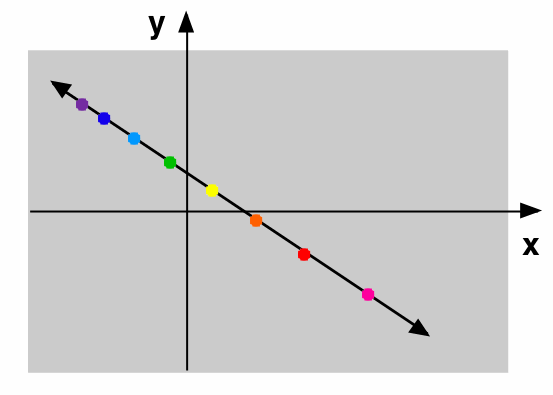
Points on the line once again remain in a line. The farther out the viewer looks, the closer together equally spaced points appear to the viewer. If the viewer keeps looking farther and farther out, the line will vanish. The point at which the image will end (the vanishing point) is the point at which a line of sight from the viewer's eye parallel to the 3D line intersects the picture plane.
Conclusion:
| The perspective image of any line that is neither parallel to the picture plane nor orthogonal to it does have a vanishing point, but that point will not be the origin. It will be wherever a line from the viewer's eye parallel to the actual 3D line passes through the picture plane. Because the vanishing point is determined by a line of sight parallel to the actual 3D line, all lines that are parallel in space share the same vanishing point in the image. |
Next!
Back to Perspective | Back to In Class Work



