And Still More Pondering


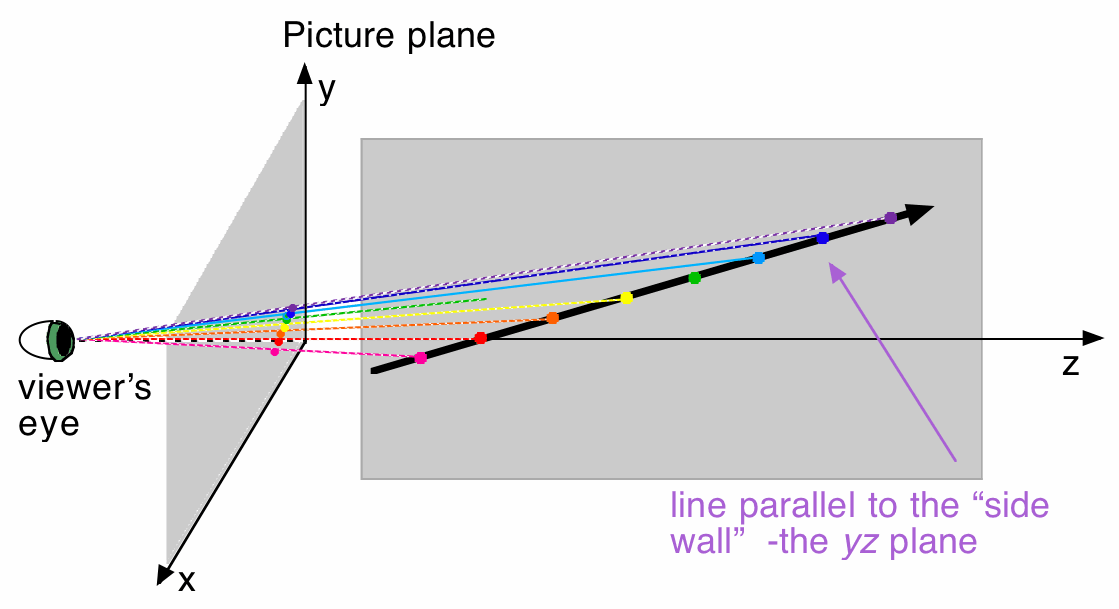
Finally, consider the specific case where a viewer is looking at a line parallel to the side wall/yz-plane. Once again, we ask: What does the viewer see?

Partial Side View (so you can see all three axes)


Straight-on Side View (so we can't see the x-axis)

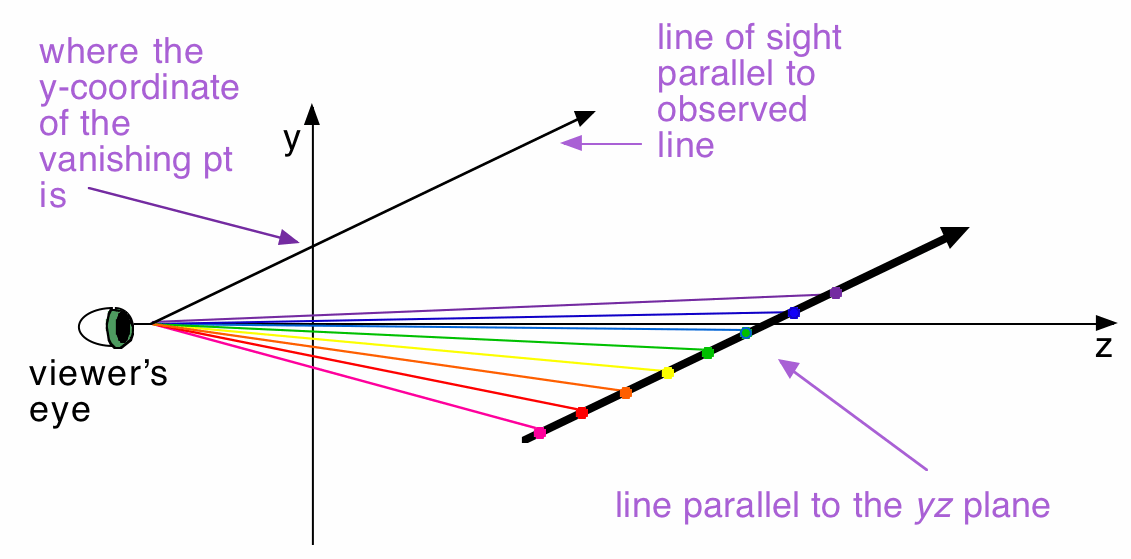
As we have now come to expect, the farther out the viewer is looking, the closer together the y-coordinates of the perspective images of the points are getting --but they are not getting closer to y=0.

The line will vanish where the line of sight that is parallel to the observed line crosses the y-axis.


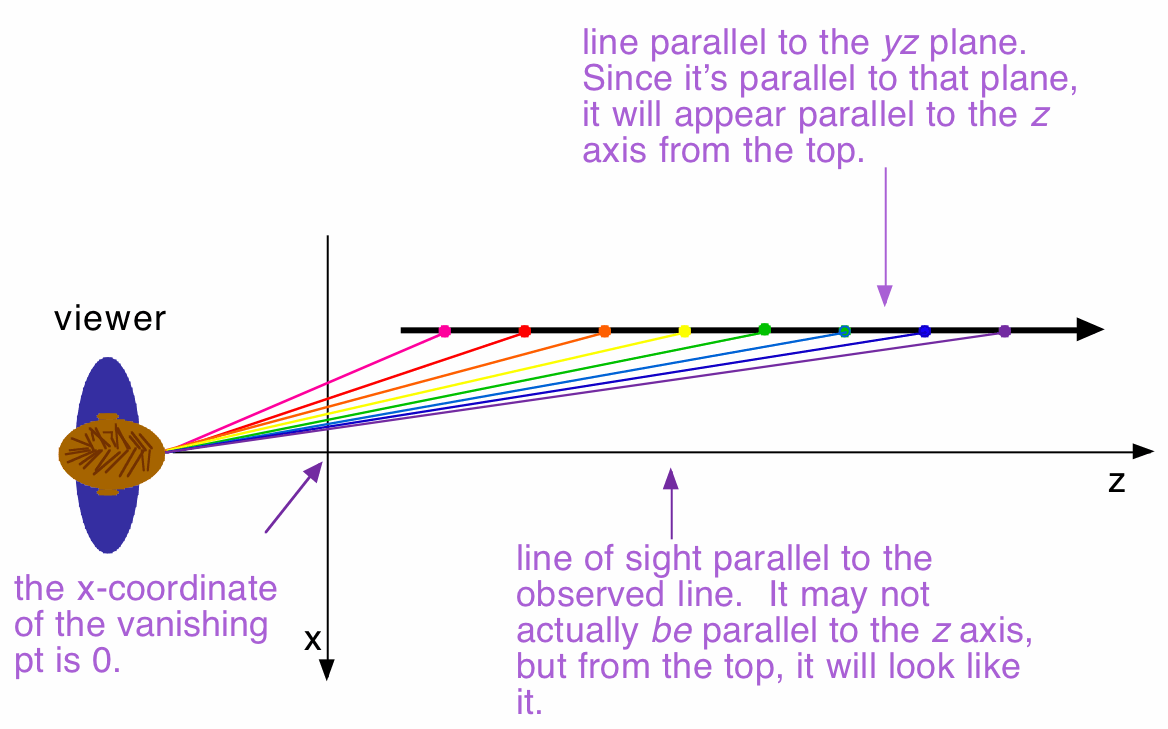
Straight-on Top View (so we can't see the y-axis)

Again, the farther out on the line the viewer looks, the closer together the x-coordinates of the images are getting-- and the closer to x=0.

The line will vanish where a line parallel to the observed line crosses the x-axis, which will be when x=0.


Front View - what the viewer sees

Let's again rotate around to see what the viewer sees:

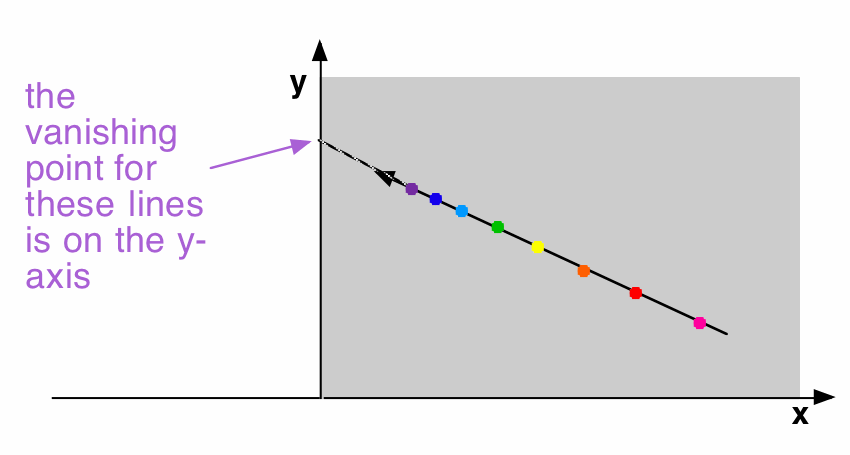
Even though the line in real-life is parallel to the side wall, the image will not be parallel to the y-axis, unless the line happens to actually lie on the yz-plane. It will move left or right toward the y-axis, where it will vanish.

The point where it vanishes is the point where a line-of-sight parallel to the actual line crosses the picture plane. Since the viewer's eye is in the yz plane, and since the actual line is parallel to that plane, such a line of sight will lie in the yz-plane, and hence will intersect the y-axis.

Conclusion:

The perspective images of lines parallel to the yz plane (that is, parallel to the side wall) have vanishing points on the y axis.

In practice, the line that plays the role of the y-axis is the vertical line through the vanishing point for orthogonals. It doesn't appear to have an official name.


Another summary

Back to Perspective | Back to In Class Work