Why?
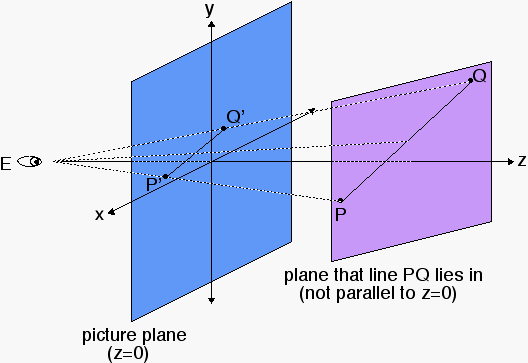
Why?
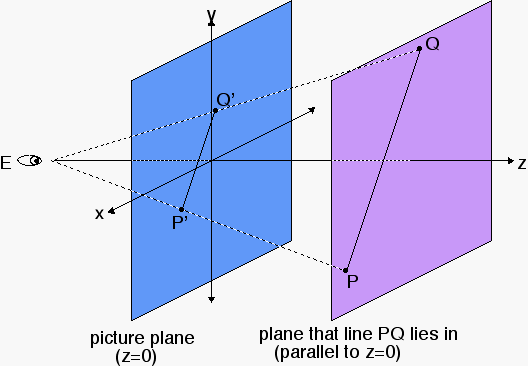
Why?
Furthermore, if these lines are orthogonal to the picture plane, their vanishing point will be the point directly opposite the ideal viewing position ("the viewer's eye"). This vanishing point is called the primary vanishing point, or the principal vanishing point.
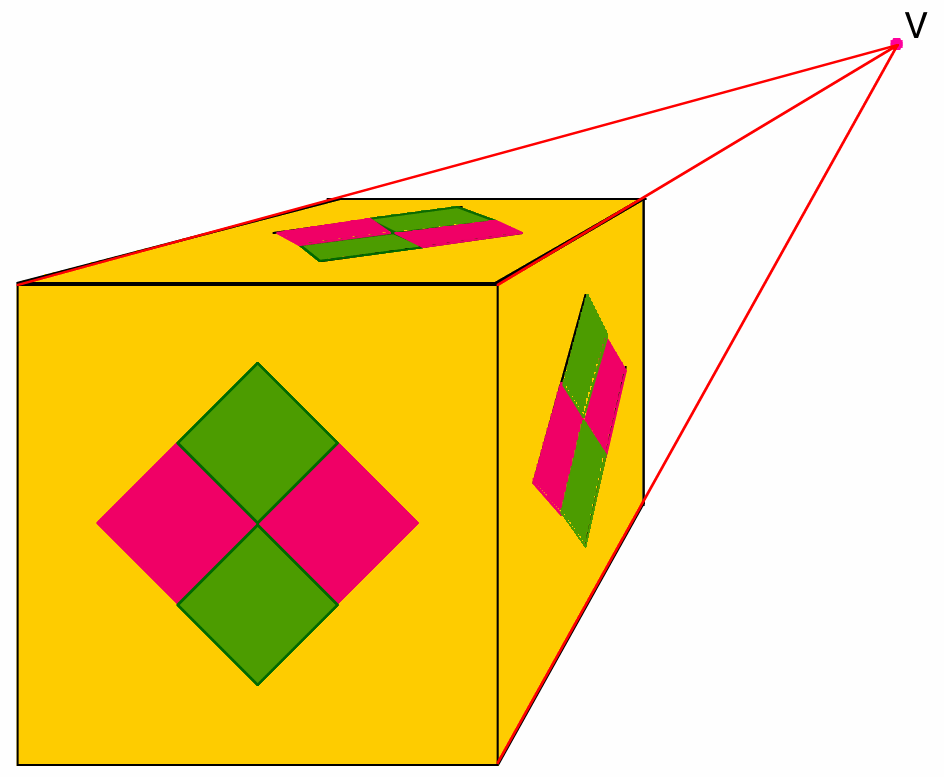
If instead, these lines lie in a plane parallel to the "floor", then their vanishing point will lie on the horizon line (the horizontal line through the primary vanishing point; i.e. through the point directly opposite the viewer's eye).
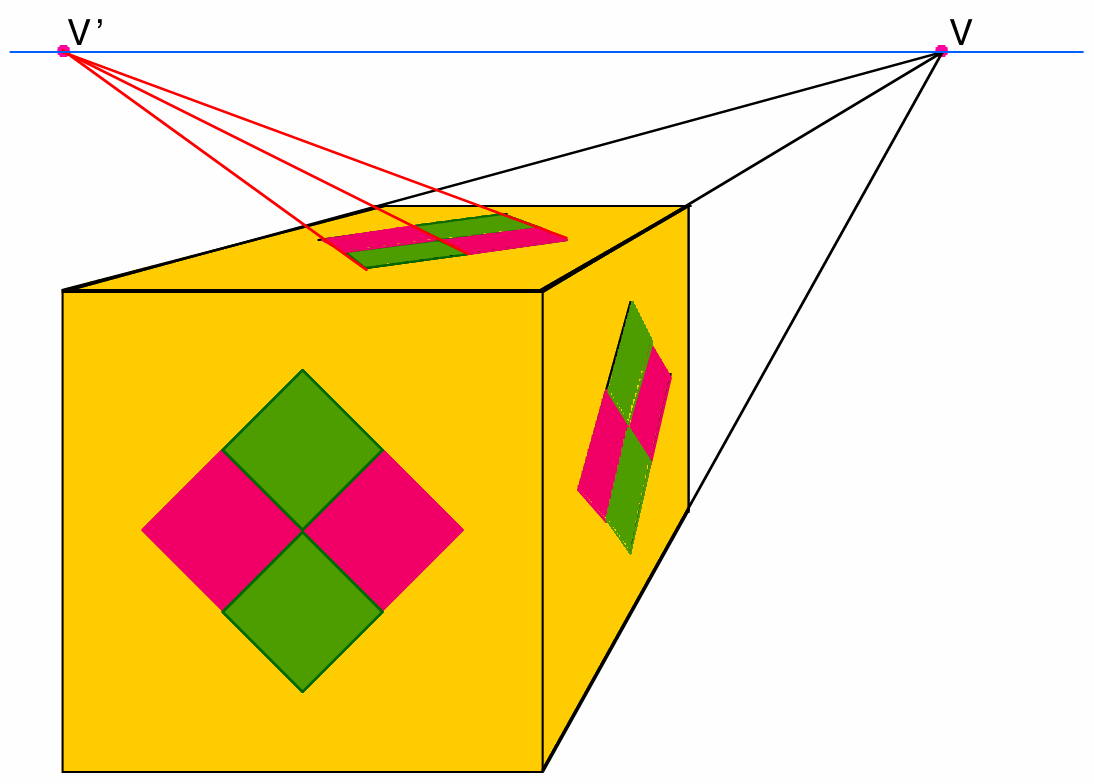
And finally, if they lie in a plane parallel to the "side walls", then their vanishing point will like on the vertical line through the primary vanishing point.
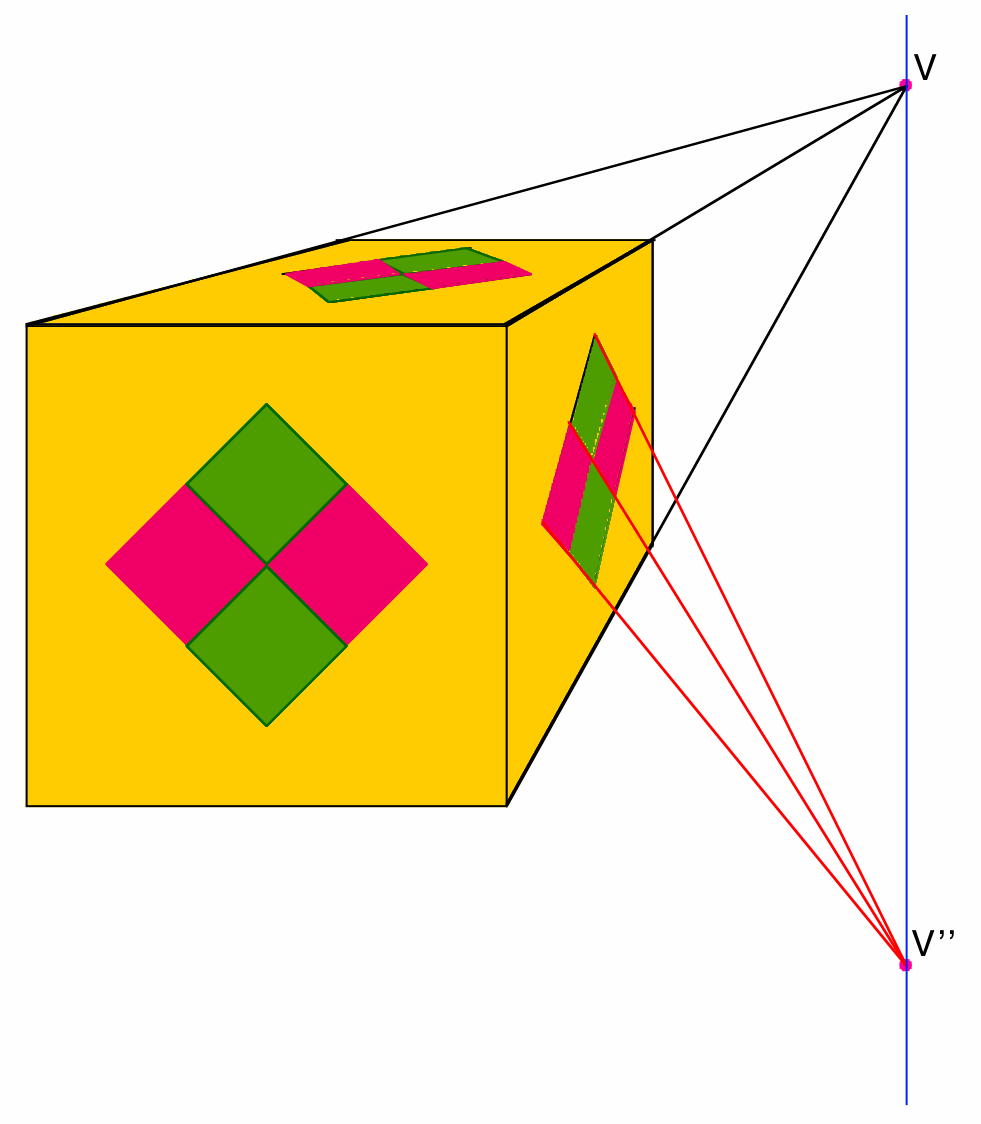
Why?
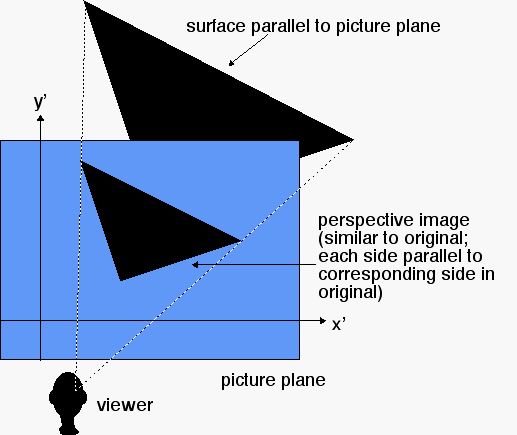
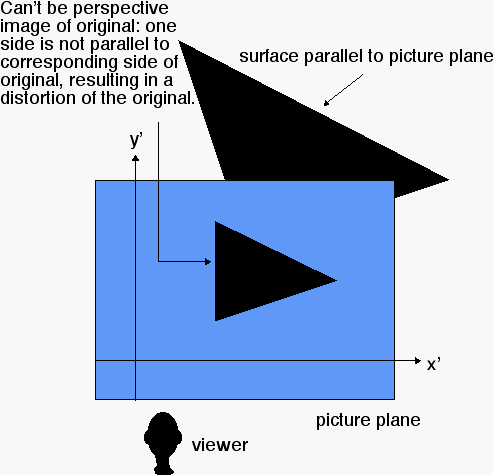
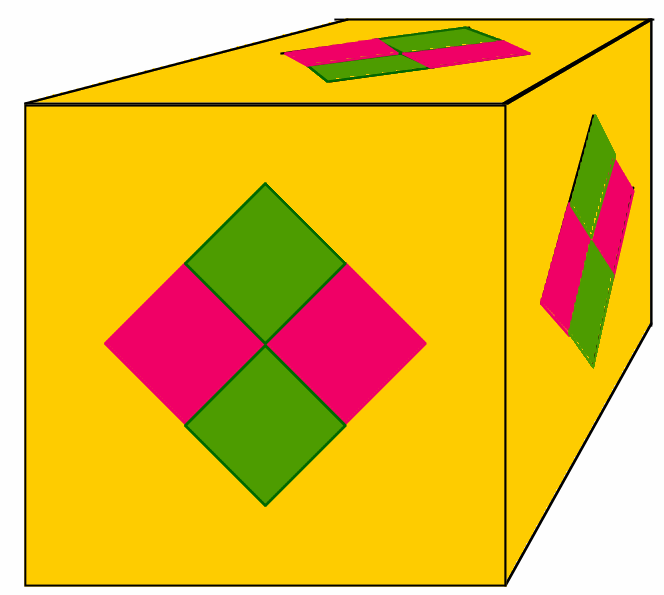
Next-using the rules of perspective to draw a cube