Why does this method work?

Finding the viewing distance - why does this method work?

	Suppose that in the painting you're looking at, there is something that you know from context is supposed to be a square that's parallel to the floor (a tile, the top of a square pillar, etc).
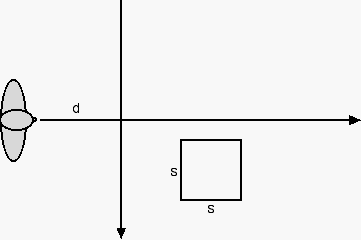
	We want to find the correct viewing distance, d.
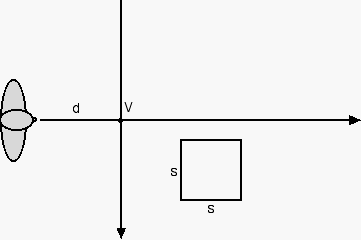
	The primary vanishing point is the point where the orthogonals^* intersect -- in other words, the point on the picture plane directly opposite the viewer's eye. Remember that orthogonals are lines in your drawing that represent lines in real space that are orthogonal (perpendicular) to the picture plane.
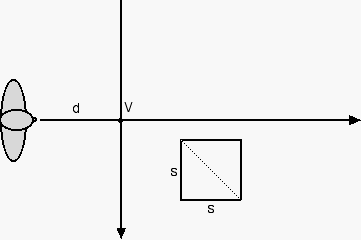
	Why does the diagonal of the square help us find the viewing distance? Let's draw it in.
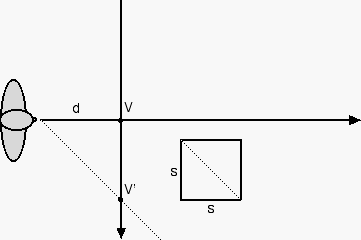
	We've seen that we can find the vanishing point for the square's diagonal by drawing the line of sight that's parallel to the diagonal. Where the line of sight intersects the x-axis (the horizon line) is the vanishing point for the diagonal, V'. We call this a secondary vanishing point.
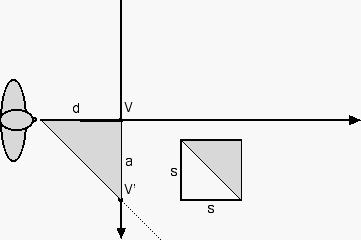
	These two diagonal lines form similar triangles (the two triangles shaded in). If we use a for the distance between V and V', we see that s/s=d/a => d/a=1 => d=a. So ... how far back from the primary vanishing point do we place ourselves? We measure the distance between the primary vanishing point and the vanishing point of the diagonal of a square that lies in the floor. That will be our ideal distance back from the primary vanishing point.