Be sure to check back often, because assignments may change!
(Last modified: Thursday, August 18, 2011, 2:45 PM )

All section and page numbers refer to sections from Calculus: Early Transcendental Functions, 3rd Edition, by Smith and Minton.

I'll use Maple syntax for some of the mathematical notation on this page. (Paying attention to how I type various expressions is a good way to absorb Maple notation). I will not use it when I think it will make the questions too difficult to read.

Due Friday 9/3 at 8am

suggestions for reading a math text
course policies
syllabus
background questionnaire, on OnCourse
WeBWorK Orientation
Introduction to Chapter 0: Preliminaries
Section 0.1: Polynomials and Rational Functions
Section 0.2: Graphing Calculators and Computer Algebra Systems
Section 0.3: Inverse Functions
Section 0.4: Trigonometric Functions
Section 0.5: Exponential and Logarithmic Functions

Note:I know this looks like a load of work, but first of all, most of the actual Calculus reading should be review, while the rest of the links shouldn't take too long (except perhaps for the WeBWorK orientation, but hopefully we make a fair amount of progress on that in lab Thursday), and second of all, you'll never have this much reading for this course again.

To read: All of the above weblinks for the course. Complete the questionnaire in OnCourse, and finish the WeBWorK orientation, which we will begin in lab Thursday. As for the introduction and the first five sections of Chapter 0, you may skip the portion of Section 0.4 on Inverse Trigonometric Functions and the portion of Section 0.5 on Hyperbolic Functions - we will leave them for Calculus 2 and Multivariable Calculus, respectively. Skim where the material seems very familiar, read more carefully where it seems new or to be presented in a different way than you are used to. Don't worry if you are not especially comfortable with some of it (especially logarithms), as long as you've seen it before. If large chunks of the material are completely unfamiliar to you, please come see me as soon as possible.

In Section 0.3, pay particular attention to the idea of one function reversing the action, or "undoing", another. Also pay attention to the distinction between the notations f ^-1(x) and [f(x)] ^-1.

In Section 0.4, make note of the table of common values of sine and cosine as they are handy to know. If these values do not look familiar to you, please come see me as soon as possible to discuss why they're true and for tips on how to remember them.

Reading questions:

1. Do you have any questions on the course policies, reading assignments, or syllabus? If so, what are they?
2. Below is a graph of the function f(x)=x⁴ +  ^x3⁄₂ - ^5x2⁄₂ + x over the interval [-1,2].
   
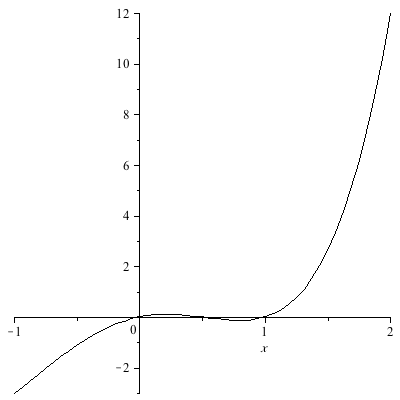
   1. What intervals for x and y satisfactorily display all the x-intercepts and local extrema of this function? (Feel free to use a graphing calculator, the on-line program Wolfram Alpha, or Maple, the Computer Algebra System Wheaton uses, which is available in A102, the computer lab, and many of the computers in the Kollett Center.)
   2. From your graph, estimate the locations of all local minima.
   3. From your graph, estimate the locations of all x-intercepts.
   4. From your graph, estimate the locations of all inflection points.
3. Can a function exist, even if you are unable to write down a precise formula for it? Give an example of how such a function might arise.
4. 1. What is the radian measure of an angle?
   2. What is 1^o, in radians?
   3. In Calculus, what unit of measure do we always use for angles?
5. How are the functions f(x)=3^x and g(x)=log₃(x) related?

Submit answers through OnCourse

Reminders:

• In these assignments, you should always briefly explain how you arrived at your answers.
• Come to lab Thursday at 1pm, in SC A102!
• Begin WW1 and PS 1, listed at the bottom of this course's web page. The problem sets due each Thursday reflect an entire week's worth of work, and you should be working on them throughout the week.
• Be working on the various assessments, which were due by 8am Wednesday, but have now been postponed to being due at 8am Friday (You don't have to have successfully passed each by then, but you do need to have completed each.)

Due Wednesday 9/8 at 8am

Problem Set Guidelines
Section 0.6: Transformations of Functions

To read: All

x Reading questions:

1. Let f(x)=x+1 and g(x)=e^x.
   1. What is the composition f o g ?
   2. What is the composition g o f ?
2. Let g(x)=2x³.
   1. How is the graph of h(x)=g(x)-5 related to the graph of g(x)? Why?
   2. How is the graph of j(x)=g(x-5) related to the graph of g(x)? Why?

Submit answers through OnCourse

Reminders:

• Continue working on the four WeBWorK assessments, which are due by 8am Friday. (They're listed in the same place as the webwork assignments, but are below the webwork assignments. Also, these assessments each have a time-limit.)
• WW1 is due Wednesday at 5pm and PS 1 is due Thursday at the beginning of lab. WeBWorK assignments are always to be done individually; although problem sets will alternate between individual and group assignments, PS 1 is an individual assignment. Read and follow the problem set guidelines referred to above.
• If you're having difficulties with the homework, or if you'd just like to make sure you're on the right track, come to my office hours and/or visit the Kollett Center during the Calc tutoring hours.
• If you have any remaining questions on the problem set after coming to my office hours and visiting the Kollett Center, bring them to class Wednesday - I will spend roughly 10 minutes at the beginning of class giving hints to the most common student questions.
• Make sure you've read all the introductory material on the course web page.

Due Friday 9/10 at 8am

Introduction to Chapter 1
Section 1.1: A Brief Preview of Calculus

To read: All

Reading questions:

1. Let y=x²+1, the parabola from Example 1.1.1.
   1. How far do you need to zoom in on the graph of y=x²+1 for it to look like a straight line at the point (2,5)? That is, what intervals for x and y should we use?
   2. Use 3 choices of second point to estimate the slope of the parabola at the point (2,5), as in Example 1.1.1. That is, find the slopes of 3 secant lines through the point (2,5), and then based on these results, make a reasonable estimate as to what the slope of the curve at the point (2,5) is.
2. (Not from the reading) What do the words limit and continuous mean to you, in every day use?
3. Give an example (not from the book) of a real-life phenomenon where there is a maximum and/or a minimum beyond which something can not go (like the size of pupils as light enters).

Submit answers through OnCourse

Reminder:

• You should have given every problem of each assessment a try by 8am Friday morning. You have until 9/17 to get 100% on each.
• Begin WW2 and PS 2. (Rather than printing out the september problem sets at one time, always go back to the web page, as I adjust the problems throughoutthe semester).
• PS 2 is a group problem set. Groups ideally consist of two people. In a pinch, three will do; more than 3 is not acceptable. Find a partner now, but most people find the group meetings work best if they begin the problems on their own, and then get together to discuss them. Do not split the problems up between you, and if any member did not substantially contribute to the best of their abilities, write a note to that effect (see the discussion of the Honor Code in the course policies.

Due Monday 9/13 at 8am

Section 1.2: The Concept of Limit

To read: All

Reading questions:

1. Consider the graphs of f(x)=^(x2-4)⁄_(x-2) and g(x)=^(x2-5)⁄_(x-2) , the two functions that the text discusses in the opening of Section 1.2.
   1. Discuss the similarities and the differences between the two graphs.
   2. If we think of what's happening at x=2 in each graph as a problem, for which function can that problem be fixed, and how (graphically)?
2. In Example 1.2.2, the authors cancel the common term of x+3 from both the numerator and the denominator, which takes a fraction which does not exist at x=-3 and turns it into one that does. And yet, a function either exists at a point or it doesn't. Why do you think it is "legal" for the authors to cancel the common term of x+3?
3. When figuring out a limit by either looking at a graph or by creating a table of nearby values, can you conclude you know that limit for sure?

Submit answers through OnCourse

Reminder:

• Just a reminder: the point of reading assignments is partially to ensure you do the reading, because multiple exposures to the material helps it sink in, partially to teach you by example how to actively read technical material (which includes asking yourself questions), and partially to give you credit for reading. I do not expect you to have mastered the section by the time you answer these questions, and do not grade on the correctness or lack thereof of your answers, only on whether your answers indicate a genuine attempt. Use this as an opportunity to identify the material you find particularly mysterious before class.
• Office Hours and/or tutoring hours are an important part of Calculus; do not hesitate to take advantage of them.

Due Wednesday 9/15 at 8am

Section 1.3: Computation of Limits

To read: All, except skip the portions of Thoerem 3.4 that relate to inverse Trigonometric Functions and skip Example 1.3.6.

Reading questions:

1. Apply the rules of limits to evaluate the following:
   1. lim_{x → 5} ^(x2-2x+7)⁄_(x-3)
   2. lim_{x→ -3}^(x2+x-6)⁄_(-x-3)
   3. lim_{x→ 1} (e^2x-1) ^1/2
2. In Example 1.3.8, what role did looking at a graph and a table of values play, and what role did using the Squeeze Theorem play?

Submit answers through OnCourse

Reminders:

• You are aiming to have received 100% on each of the assessments by 9/17. If you've been giving it every effort but are having trouble, please come talk to me.
• Your group will turn in one joint version of PS 2; the recopying should all be done by one person, the "primary author". Put a star next to the name of the "primary author".
• If, after coming to office hours, you still have questions on PS 2, bring them to class on Wednesday.
• Be sure that each member of your group has a photocopy of the problem set you turn in, both for studying purposes and for your records.
• I suggest that you switch partners with every group problem set. You should be the primary author roughly every other group problem set.

Due Friday 9/17 at 8am

Section 1.4: Continuity and its Consequences

To read: All. In the discussion of the tax rate schedule that precedes Example 1.4.8, work to understand where the piecewise-defined function comes from, and then be sure to understand Example 4.8 itself.

Reading questions:

1. Let f be a function.
   1. True or false (and why): If f(a) exists, f must be continuous at x=a.
   2. True or false (and why): If lim_{x → a} f(x) exists, then f must be continuous at x=a.
2. When a function f is continuous at x=a, how can you compute lim_{x →a} f(x)? Why should you not use this technique when the function is discontinuous at x=a?
3. In Example 1.4.2, if we define g(1)=7, is g(x) continuous at x=1? Why or why not?
4. Why are the discontinuities in Figure 1.22b and Figure 1.22d not removable?
5. Without looking at a graph, how can we conclude that f(x)=e^cos(x)-1 has a zero on the interval [- ^π⁄₂,0]?

Submit answers through OnCourse

Due Monday 9/20 at 8am

Section 1.5: Limits Involving Infinity; Asymptotes
Section 1.7: Limits and Loss of Significance Errors

To read: All of Section 1.5, except for Example 1.5.10. As for Section 1.7, I'd just like you to skim through it, to get a feel for what can go wrong when relying on a computer or a calculator without understanding what it's doing.

Reading questions:

1. Does lim_{x → -3} ¹⁄_(x+3)⁴   exist? If so, what is it? If not, why not?
2. Discuss the left- and right-sided limits for lim_{x → 4} ^(x-1)(x-3)⁄_(x-6)(x-4).

Submit answers through OnCourse

Reminders:

• Begin WW3 and PS 3. PS 3 is an individual assignment.
• I just want to remind you again to take advantage of both my office hours and the Kollett Center!
• In this course, we will occasionally skip sections. We will be skipping Section 1.6, as I believe this material can wait until a later course (for those who continue on).

Due Wednesday 9/22 at 8am

Introduction to Chapter 2
Section 2.1 Tangent Lines and Velocity

To read: All

Reading questions:

1. Describe in your own words what a secant line and a tangent line to a curve is.
2. Can a tangent line intersect a curve at more than one point?
3. Let f(x)=x²+x.
   1. Find the slope of the secant line from x=1 to a nearby point x=1+h.
   2. For the above secant line, must the value of h be positive? (Explain)
4. Briefly explain the difference between speed and velocity.

Submit answers through OnCourse

Reminders:

• Bring remaining questions on PS 3 to class.

Due Friday 9/24 at 8am

Section 2.2: The Derivative

To read: All. Be sure to pay particular attention to Examples 2.2.5 and 2.2.6--these examples are extremely important as they illustrate, much more than any formula can, what is really going on with derivatives.

Reading questions:

1. In the first paragraph of the section, the authors say that the fact that otherwise unrelated notions can be described by the same mathematical expression is an indication of the power of mathematics. Why do you think this is an indication of math's power?
2. Let f(x)=2x²-3x .
   1. Mimic Example 2.2.1 to compute the derivative of f(x) at x=1.
   2. Mimic Example 2.2.2 to compute the derivative of f(x) at an unspecified value of x. Use your result to compute the derivative of f(x) at x=1, x=2, and x=3.

      For those of you who have learned derivatives before: You may know a shorter way of doing this problem. Nonetheless, please proceed as in Example 2.2.1, to practice the ideas of the definition of the derivative.

3. In many of the examples in the text, and in the previous reading question, we find the derivative of a function at an unspecified point. What is the benefit of doing this?
4. The graph of a function g(x) is shown below.
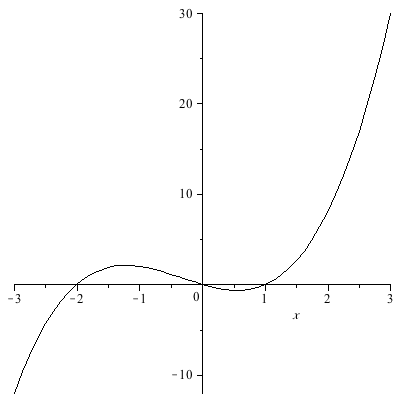
   1. On what intervals of x is the slope of the tangent line positive?
   2. On what intervals of x is the slope of the tangent line negative?

Reminder:

• Start working on WW4 and PS4. PS4 is your second group assignment -- most people find that it's a really good idea to work with somebody different each time for the first many group problem sets. If you were not the primary author last time, you should be this time. Do not split up the problems between you.

Due Monday 9/27 at 8am

Section 2.3: The Power Rule

To read: All

Reading questions:

1. What is the slope of the line tangent to y=2x?
2. Let f(x)=-5x²+7x-4. Compute as many derivatives as possible, as in Example 3.6.
3. Let g(x)=⁵⁄_x². Compute g ', g '', g '''. Why am I not asking you to compute as many higher-order derivatives as possible, as in the previous question and Example 3.6?

Submit answers through OnCourse

Due Wednesday 9/29 at 8am

Section 2.4: The Product and Quotient Rules

To read: All.

Reading questions:

1. The second sentence of the section says "...you might wonder whether the derivative of a product of two functions is the same as the product of the derivatives." Why might you think that?
   
2. Find the derivative of (³⁄_x² - √ x)(6x³+8x²-14).
3. Find the derivative of ^{(3⁄_x2 - √ x)} ⁄_{(6x³+8x²-14)}.

Submit answers through OnCourse

Reminders:

• Bring remaining questions on PS 4 to class.
• Remember to put a star next to the primary author's name on the final version of PS 4.
• Exam 1 will be Thursday 10/7.