Be sure to check back often, because assignments may change!
(Last modified: Wednesday, April 2, 2008, 9:54 AM )

I'll use Maple syntax for mathematical notation on this page.
All section and page numbers refer to sections from Smith & Minton's Multivariable Calculus, 3rd edition.

Due Monday 3/3 at 9am

Review Sections 12.1-12.3

• To read: Re-read

No Reading Questions today!

Reminders:

• The take-home portion of Exam 1 is due Monday at 4:30 .

Due Wednesday 3/5 at 9am

12.4: Tangent Planes and Linear Approximations

• To read: All. Don't obsess too much over the details of the section on Increments and Differentials, but do read it, as it leads to the definition of what we mean by being differentiable at the point (a,b).

E-mail Subject Line: Math 236 Your Name 3/5

Reading questions:

1. If f(x,y) is a well-behaved function and has a local maximum at (a,b), what can you say about the linear approximation to f(x,y) at (a,b)?
2. Let f(x,y)=xy^2. Find a vector normal to the plane tangent to z=f(x,y) at the point (2,3,18).
3. Let L(x,y) be the linear approximation of f(x,y) at (a,b). What graphical properties of the surface z=f(x,y) would make L(x,y) particularly accurate? particularly inaccurate?

Reminder:

• PS 5 is again a group assignment. Once again, switch to all new partner(s). As always, don't split problems up between you.

Due Friday 3/7 at 9am

Section 12.5: The Chain Rule

• To read: All

E-mail Subject Line: Math 236 Your Name 3/7

Reading questions:

Suppose that w=f(x,y,z) and that x,y, and z are all functions of r,s, and t.
1. How many partial derivatives do you need to calculate to determine ∂w/∂t? (Using a tree diagram may prove useful.)
2. What is the expression for ∂w/∂t?

• Star the primary author's name on PS 5.
• E-mail me by Friday at 3pm to let me know which project option you're choosing.

Monday 3/10 through Friday 3/14

Enjoy your spring break!

Due Monday 3/17 at 9am

Section 12.5: The Chain Rule (continued)

• To read: Re-read the section, to refresh your memory after break!

No Reading Questions today!

Reminder:

• Get started on the project. The first substantive deadline is Friday.

Due Wednesday 3/19 at 9am

Section 12.6: The Gradient and Directional Derivatives

• To read: Read through Example 6.3 (page 987)

E-mail Subject Line: Math 236 Your Name 3/19

Reading questions:

1. In order to find D_uf(a,b), what must be true about our choice of u?
2. What type of quantity is the gradient of f? If we have z=f(x,y) is a surface in 3 dimensions, then what dimension does the gradient live in?
3. For f(x,y)=x^2y-4y^3,
   

   (a) Compute D_uf(2,1) for u=<-3/5,4/5>.
   (b) Compute the gradient of f(x,y)

Due Friday 3/21 at 9am

Section 12.6: The Gradient and Directional Derivatives (continued)

• To read: Finish the section

Reading questions:

1. Toward the top of page 988, the book says:

   ..notice that a zero directional derivative at a point indicates that u is tangent to a level curve.

   Why is this true?
2. What information does the gradient give you about f(x,y)?

Reminders:

• Turn in the first stage of the project by 3pm.

Due Monday 3/24 at 9am

Section 12.6: The Gradient and Directional Derivatives (continued)

• To read: Re-read the whole section -- there are a lot of subtle ideas in this section.

No Reading Questions Today

Due Wednesday 3/26 at 9am

Section 12.7: Extrema of Functions of Several Variables

• To read: Through example 7.3 (bottom of page 1001)

E-mail Subject Line: Math 236 Your Name 3/26

Reading questions:

1. If the partials f_x and f_y exist everywhere, at what points can f have a local max or a local min?
2. Suppose f_x(x₀, y₀)=f_y(x₀, y₀)=0, and at that same point both f_xx and f_yy are positive (so that in both the x and y direction, f is concave up). Must f have a local min at the point (x₀, y₀)?
3. Suppose that f is a "nice" function, and that the following are true:
   • f_x(2,-1)=0=f_y(2,-1)
   • f_xx(2,-1)=-1
   • f_yy(2,-1)=-3
   • f_xy(2,-1)=2.5
   Will the point (2,-1) be a local max, local min, neither, or do you not have enough information to tell? In any case, justify your answer.

Reminders:

• PS 7 is again a group assignment. As always, switch partners, don't divide the problems up, and put a star next to the primary author's name.

Due Friday 3/28 at 9am

Section 12.7: Extrema of Functions of Several Variables (continued)

• To read: Finish the section

E-mail Subject Line: Math 236 Your Name 3/28

Reading questions:

1. Describe the idea behind the method of steepest ascent in your own words.

Due Monday 3/31 at 9am

Section 13.1: Double Integrals

• To read: All

E-mail Subject Line: Math 236 Your Name 3/31

Reading questions:

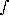
1. If f(x,y) is a positive function of two variables, what does 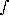_R f(x,y)dA measure?
2. Explain Fubini's Theorem in your own words. What is its importance?

Reminder:

• The next stage of the project is due Wednesday at 3pm.