Be sure to check back often, because assignments may change!
(Last modified: Monday, February 22, 2010, 9:55 AM )

I'll use Maple syntax for mathematical notation on this page.
All section and page numbers refer to sections from Smith & Minton's Multivariable Calculus, 3rd edition.

Due Friday 1/29 at 9am

guidelines for submitting reading assignments
suggestions for reading a math text
course policies
syllabus
Fill out the questionnaire on my OnCourse page

• To read: all
• Pay attention to: all of it. Any questions? Please do ask me!

Section 10.1: Vectors in the Plane
Section 10.2: Vectors in Space
Section 10.3: The Dot Product

• To read: All of sections 10.1 and 10.2; up thru the middle of p. 808 in Section 10.3. Don't worry, you won't usually have this much to read!
  In this course, the graphs and diagrams are critical, and the authors really put a lot of effort into explaining them. Many people have a hard time plotting points on 3D axes (see section 10.2) -- really try to follow what the authors are describing in their diagrams!

E-mail Subject Line: Math 236 Your Name 1/29

Reading questions:

1. Find a unit vector in the direction of <-2,3,-6>.
2. Let a=<2,-1,3>, b=<4,10,-1>, and c=<3,-1,2> be vectors, and let x.y represent the dot product of any vectors x and y.
   

   (a) Find a.b.
   (b) Does (a.b).c make sense, and if so, what is it in this case?
   (c) Are b and c orthogonal?
   

Reminders:

(I start out with extensive reminders at the beginning of the semester -- often things I'm afraid I'll forget to mention. I pare them down significantly as the semester goeos by.)

• In these assignments, you should always briefly explain how you arrived at your answers.
• Remember, if you have any questions, please come to my office hours. Office hours will probably be a huge part this class; I expect nearly every one will come see me at least every couple weeks.
  
• Begin Problem Set 1, listed at the bottom of this course's web page. . The problem sets that are due each Friday (except this first Friday, 1/29) reflect an entire week's worth of work, and you should be working on them throughout the week. PS 1, due 2/5, will actually reflect more than a week's worth of work, and as such will be unusually long, so plan on spending plenty of time on it!

Please Note:

You should eventually receive an automated response letting you know I've received your reading assignment -- once I've received it, which doesn't happen unless my laptop is awake and my e-mail is open. But you'll only receive that message if your subject headings exactly match the filters I've set up. If you don't receive such a message, it might mean I didn't get your response, but it might also just mean that your subject heading didn't match my filters.

Occasionally check the grades available through OnCourse to see whether I've gotten all your reading assignments: sometimes messages do seem to just disappear. (Note: I do not use the OnCourse grade sheet for anything other than letting you know scores, so don't pay any attention to the totals.)

Due Monday 2/1 at 9am

Multi Problem Sets
Problem Set Guidelines
Section 10.4: The Cross Product

• To read: Finish Section 10.3; read 10.4 thru page 821.

E-mail Subject Line: Math 236 Your Name 2/1

Reading questions:

1. Briefly explain what, geometrically, proj_ba and comp_ba are.
2. How is a x b related to a and b geometrically?
3. If a and b are vectors in V₂ (that is, in the plane), is a x b defined?
4. If a, b, and c are arbitrary vectors, should we expect that (a x b) x c=a x (b x c)?

Reminder:

• For the problem sets, it really is a good idea if you work on the practice ("black") problems first -- I choose those to be good problems for helping with understand the ideas and techniques. You'll find that writing up the focus ("red") problems goes much more smoothly if you've already worked through the practice problems.
• PS 1 is an individual assignment. While this of course means that you will each be turning in your own problem set, it does not mean that you can not work with someone else, as long as you do so in a way that helps you all better understand the material. This generally means that you each think about the problems on your own, and then discuss your ideas. It often will also mean working through the problems on your own, and then comparing results. When it comes time to write the problems up, you should each do so on your own. Just to be clear: You absolutely may not divide the problems up between you, nor may you copy somebody else's work, merely changing a word or two (see the section on the Honor Code in the Course Policies).

• Make sure you've read Multi Problem Sets and Problem Set Guidelines.

Due Wednesday 2/3 at 9am

Section 10.4: The Cross Product

• To read: Finish Section 10.4. You will notice throughout this book that there are many applications -- in section 10.4, you encounter torque and magnus force. We won't always be able to spend much time on the applications, but still read them to get a sense of the place of multivariable calculus in the world. Those of you with a related background (in this case, physics) will probably get more out of these applications than others; if the details of such examples prove stressful, focus on the big picture.

E-mail Subject Line: Math 236 Your Name 2/3

Reading questions:

1. How can we tell whether two vectors in V₃ are parallel? How can we tell whether two vectors are orthogonal?

Reminder:

• Make sure you clear up any difficulties on PS 1 by coming to my office hours or taking advantage of the tutors at the Kollett Center.

Due Friday 2/5 at 9am

Section 9.1: Plane Curves and Parametric Equations
Section 10.5: Lines and Planes in Space

• To read: Read all of Section 9.1 (available through my OnCourse page); through middle of page 832 in Section 10.5.

E-mail Subject Line: Math 236 Your Name 2/5

Reading questions:

1. What information about a line L do you need to determine an equation for the line?
2. Find parametric equations for the line through the point (1,2,3) and parallel to the vector <3,0,-1>.
3. Find parametric equations for the line through the points (1,2,3) and (7,-1,0).
4. What information about a plane P do you need to determine an equation for the plane?
5. Find an equation for the plane containing the point (1,2,3) with normal vector <3,0,-1>.

Reminder:

• PS 1 is due at the beginning of class Friday.
• Quick reminder: the problem sets that are due each Friday reflect the whole week's worth of work, and should be worked on throughout the week, so plan on starting PS 2 this week-end. As always, start with the practice problems. It's a group problem set, so find a partner to work with now, to work with after you've given some thought to the problems. (You must work in a group. Groups of 2 are best; 3 is less than ideal, but sometimes unavoidable. I do not want you to turn in a hw you've done on your own, neither do I want you to work in a group of 4.) As always, don't split the problems up between you.

Due Monday 2/8 at 9am

Section 10.5: Lines and Planes in Space
Section 11.1: Vector-Valued Functions

• To read: Finish reading Section 10.5; In Section 11.1, read everything but Example 1.8. Really think about Example 1.5 -- before you ever turn the page, can you make some progress on figuring out which vector-valued functions do (or do not) go with which graphs?

  By the way, when the book refers to past sections that you haven't studied, don't panic -- just figure out as much as you can about it, and move on.

E-mail Subject Line: Math 236 Your Name 2/8

Reading questions:

1. The vector-valued function r(t)=cos(t)i+sin(t)j lies in the plane.

   (a) Using Example 1.2 as a guide, what will the graph of this function look like?
   (b) Is it possible to rewrite r(t) as a function y=f(x)?

2. What are some advantages to using vector-valued functions?

Reminders:

• Check out the tutoring hours for Multi at the Kollett Center office hours held by student tutors.

Due Wednesday 2/10 at 9am

Section 11.2: The Calculus of Vector-Valued Functions

• To read: All.

E-mail Subject Line: Math 236 Your Name 2/10

Reading questions:

1. If r(t)=tcos(t)i+exp(t^2)j+ln(t)k, what is r'(t)?
   Remember exp(t^2) is Maple notation for e^t2.
2. If r(t) is a vector-valued function, what geometric/graphical information does r'(a) give you?
3. Let r(t)=cos(t)i+sin(t)j and s(t)=sin(5t)i+cos(5t)j.

   (a) What do the graphs of r(t) and s(t) look like?
   (b) If the graphs of two vector-valued functions r(t) and s(t) are the same, must r'(0)=s'(0)? (Is this a new result, or was it also true for functions f(x) and g(x)?)

Reminders:

• For the group problem sets, each group will turn in one joint problem set. You should work together to solve every problem, then one of you should take responsibility for writing up the entire problem set. That person is the "primary author". On the finished problem set, put a star next to the primary author's name.
• These groups are not permanent -- you'll be switching partners from week to week. You should end up being primary author 1/3 - 1/2 the time (depending on whether you're working in groups of 2 or 3).

Due Friday 2/12 at 9am

Problem Set Guidelines
Section 11.3: Motion in Space

• To read: Review the Problem Set Guidelines again before turning in PS 2. Read all of Section 11.3. Pay particular attention to Examples 3.4 and 3.7. We probably won't spend much time on rotational motion, but still skim through those examples (3.3, 3.5, and 3.6).

E-mail Subject Line: Math 236 Your Name 2/12

Reading questions:

1. If r(t) is a vector-valued function representing the motion of an object at time t, what physical information does r'(t) give you? How about ||r'(t)||?
2. Find the velocity and acceleration vectors, if the position of an object moving in space is given by r(t)=(5/sqrt(t))i+ln(t³)j-tan(3t)k.

Reminders:

• Make sure each member of your group has a photocopy of the problem set (for studying purposes).
• (From Wednesday 2/10:) I had hoped to incorporate a little bit of work with Maple, on laptops Friday. As I adjust my plan for Friday to take into account where we are, it looks like there may be a short opportunity to use it to help with some in-class work at the end of class. It's completely up to you whether you think it's worth it to bring it to class for something we might or might not get to! If not enough people bring them, I'll just post a file that shows useful commands, as I often do.

Due Monday 2/15 at 9am

11.3: Motion in Space

• To read: Re-read Section 11.3.

No Reading Questions Today

Reminders:

• Just a reminder that you are responsible for all of the practice problems, and that you really will find the focus problems easier if you work through the practice problems first.

Due Wednesday 2/17 at 9am

Anton, Bivens, and Davis Section 13.3: Change of Parameter; Arclength
Section 11.4: Curvature

• To read: Read all of Section 13.3 from the Multivariable Calculus book by Anton, Bivens, and Davis, available through my OnCourse page. In Section 11.4, read through Example 4.2, top of page 889.

E-mail Subject Line: Math 236 Your Name 2/17

Reading questions:

1. Consider the circle r(t)=cos(t)i+sin(t)j.
   • (a) Find a change of parameter t=h(τ) such that the circle is traced counter-clockwise as τ increases over the interval [0,1/2].
   • (b) Use the chain rule for vector-valued functions to differentiate r(τ).
   • (c) Does the change of parameter you found preserve orientation or reverse it?
2. Let r(t)=t³i+sin²(t)j.
   • (a) The graph of r(t) is displayed below, with arrows super-imposed attempting to show the tangent vectors (the lenths are all wrong, but the direction is all that matters here anyway). Based on the graph, does r(t) have a continuously turning tangent vector?
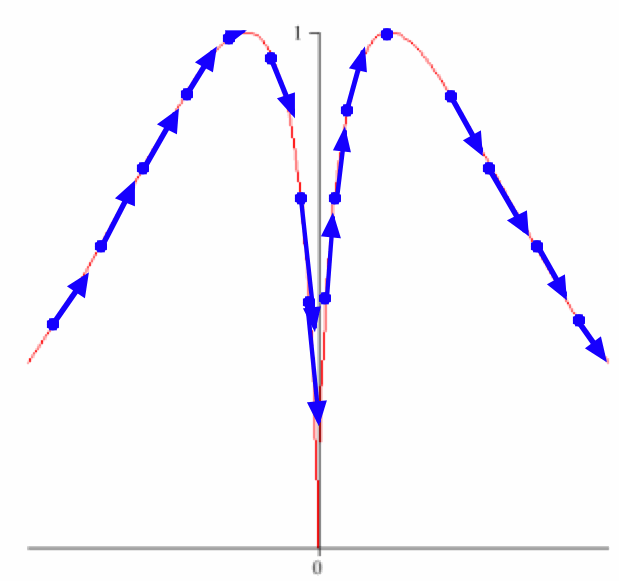
   • (b) Verify your answer algebraically.

Reminders: